Дифференциальное уравнение Бернулли и методы его решения
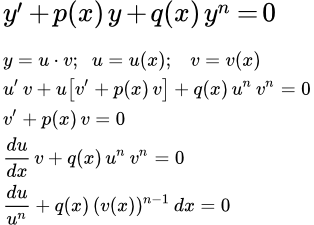
- Дифференциальное уравнение Бернулли
- – это уравнение вида:
, где n ≠ 0, n ≠ 1, p и q – функции от x.
Решение дифференциального уравнения Бернулли приведением к линейному уравнению
Рассмотрим дифференциальное уравнение Бернулли:
(1) ,
где n ≠ 0, n ≠ 1, p и q – функции от x.
Разделим его на y n. При y ≠ 0 или n < 0 имеем:
(2) .
Это уравнение сводится к линейному с помощью замены переменной:
.
Покажем это. По правилу дифференцирования сложной функции:
;
.
Подставим в (2) и преобразуем:
;
.
Это – линейное, относительно z, дифференциальное уравнение. После его решения, при n > 0, следует рассмотреть случай y = 0. При n > 0, y = 0 также является решением уравнения (1) и должно входить в ответ.
Решение методом Бернулли
Рассматриваемое уравнение (1) также можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:
y = u·v,
где u и v – функции от x. Дифференцируем по x:
y′ = u′ v + u v′.
Подставляем в исходное уравнение (1):
;
(3) .
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Уравнение (4) – это уравнение с разделяющимися переменными. Решаем его и находим частное решение v = v(x). Подставляем частное решение в (3). Поскольку оно удовлетворяет уравнению (4), то выражение в круглых скобках обращается в нуль. Получаем:
;
.
Здесь v – уже известная функция от x. Это уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv.
Примеры решений дифференциального уравнения Бернулли
Пример 1
Решить уравнение
(П1.1)
Решение
Это дифференциальное уравнение Бернулли. Решаем его методом Бернулли. Ищем решение в виде произведения двух функций: . Тогда
. Подставляем в (П1.1):
;
(П1.2) .
Одну из этих функций мы можем выбрать произвольным образом. Выберем v так, чтобы выражение в круглых скобках равнялось нулю:
(П1.3) .
Тогда подставляя (П1.3) в (П1.2), мы получим дифференциальное уравнение с разделяющимися переменными:
(П1.4) .
Сначала мы определим функцию v. Нам нужно найти любое, отличное от нуля, решение уравнения (П1.3). Решаем его. Для этого разделяем переменные и интегрируем.
;
;
;
;
.
Отсюда , или . Возьмем решение с и знаком ′плюс′. Тогда , или .
Подставим в (П1.4), разделяем переменные и интегрируем:
(П1.4) ;
;
;
.
При имеем:
;
;
;
;
.
Итак, мы нашли функции u и v. Находим искомую функцию y:
.
Заменим постоянную интегрирования: . Тогда общее решение исходного уравнения (П1.1) примет вид:
.
Когда мы делили на u, то предполагали, что . Теперь рассмотрим случай . Тогда . Нетрудно видеть, что постоянная функция также является решением исходного уравнения (П1.1) ⇑.
Ответ
Общее решение уравнения: .
Уравнение также имеет решение .
Пример 2
Решить уравнение
Решение
На первый взгляд, кажется, что это дифференциальное уравнение не похоже на уравнение Бернулли. Если считать x независимой переменной, а y – зависимой (то есть если y – это функция от x), то это так. Но если считать y независимой переменной, а x – зависимой, то легко увидеть, что это – уравнение Бернулли.
Итак, считаем что x является функцией от y. Подставим в исходное уравнение и умножим на :
;
;
(П2.1) .
Это – уравнение Бернулли с n = 2. Оно отличается от рассмотренного выше, уравнения (1), только обозначением переменных (x вместо y). Решаем методом Бернулли. Делаем подстановку:
x = u v,
где u и v – функции от y. Дифференцируем по y:
.
Подставим в (П2.1):
;
(П2.2) .
Ищем любую, отличную от нуля функцию v(y), удовлетворяющую уравнению:
(П2.3) .
Разделяем переменные и интегрируем:
;
;
.
Поскольку нам нужно любое решение уравнения (П2.3), то положим C = 0:
; ; .
Возьмем решение со знаком ′плюс′:
.
Подставим в (П2.2) учитывая, что выражение в скобках равно нулю (ввиду (П2.3)):
;
;
.
Разделяем переменные и интегрируем. При u ≠ 0 имеем:
;
(П2.4) ;
.
Во втором интеграле делаем подстановку :
;
.
Интегрируем по частям:
;
.
Подставляем в (П2.4):
.
Возвращаемся к переменной x:
;
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
