Примеры решений дифференциальных уравнений второго порядка методом Лагранжа
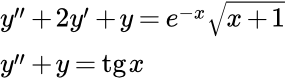
Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>>.
Пример 1
Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)
Решение
Шаг 1. Решение однородного уравнения
Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:
Это уравнение второго порядка.
Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .
Шаг 2. Вариация постоянных – замена постоянных функциями
Варьируем постоянные C1 и C2. То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .
Находим производную:
.
Свяжем функции и уравнением:
(6) .
Тогда
.
Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;
.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .
Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .
Решение системы уравнений
Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.
Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:
.
По формулам Крамера находим:
;
.
Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .
.
.
Общее решение исходного уравнения:
;
.
Ответ
.
Пример 2
Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)
Решение
Шаг 1. Решение однородного уравнения
Решаем однородное дифференциальное уравнение:
(9)
Ищем решение в виде . Составляем характеристическое уравнение:
Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .
Шаг 2. Вариация постоянных – замена постоянных функциями
Теперь варьируем постоянные C1 и C2. То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .
Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .
Решение системы уравнений
Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.
Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:
.
По формулам Крамера находим:
;
.
Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования тригонометрических функций).
Второй интеграл табличный (см. Таблица неопределенных интегралов).
.
Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :
.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.
Общее решение исходного уравнения:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
