Теорема Коши существования и единственности решения дифференциального уравнения первого порядка
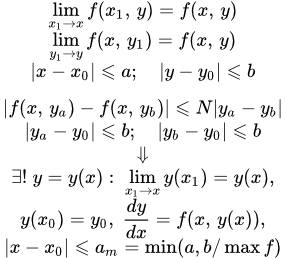
Впервые существование решения дифференциального уравнения было доказано Коши. Приводимое ниже доказательство основано на методе последовательных приближений, который принадлежит Пикару. Этот метод имеет самостоятельное значение, поскольку позволяет получить приближенное решение дифференциального уравнения.
Формулировка теоремы
Пусть дано дифференциальное уравнение первого порядка:
(1)
с начальным условием
(1.1) .
Пусть – непрерывная функция двух переменных в замкнутой области :
и, следовательно, ограничена некоторым положительным значением :
(2) .
И пусть функция удовлетворяет условию Липшица:
(3) ,
.
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальному условию , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .
Условие Липшица
Рассмотрим условие Липшица. Оно имеет вид:
(3) ,
где – положительное число;
, и – любые значения из области :
, , .
Смысл условия Липшица легко понять, если записать его в виде:
(3.1) .
При некотором фиксированном значении переменной , функция является функцией от переменной : . Пусть мы имеем график этой функции. Возьмем две точки, принадлежащие , на этом графике и проведем через них прямую. Тогда угол между прямой и осью ограничен некоторым значением , которое меньше . При таком ограничении график не имеет вертикальных касательных и скачков. А в тех точках, где существует частная производная , она ограничена:
.
Если в области функция имеет непрерывную частную производную , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частная производная непрерывна в замкнутой области, то она ограничена:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой переменная принадлежат интервалу между и :
.
Тогда:
.
Доказательство существования решения
Приведем исходное уравнение (1) с начальным условием (1.1) к интегральному уравнению. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем это уравнение по от до :
;
Подставим начальное условие . В результате получим интегральное уравнение:
(4) .
Покажем, что интегральное уравнение (4) эквивалентно дифференциальному уравнению (1) с начальным условием (1.1). Для этого нужно показать, что из (1) и (1.1) следует (4) и из (4) следует (1) и (1.1). То, что из (1) и (1.1) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.1). Для этого подставим в (4) . Получим начальное условие (1.1). Продифференцировав обе части уравнения (4) по , получаем уравнение (1).
Далее мы пытаемся найти решение уравнения (4) с помощью последовательных приближений. Для этого определяем ряд функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.........
(5.n) .
Мы предполагаем, что при , стремится к решению уравнения (4):
(6) ,
где – решение уравнения (4). Если мы докажем это, то мы докажем существование решения.
Доказательство существования решения будем проводить в два этапа:
1} вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет уравнению (4):
.
1) Доказательство существования предела yn при n стремящемся к бесконечности
Сведем последовательные приближения (5.1) – (5.n) к сумме ряда. Для этого пишем:
.
Таким образом нам нужно доказать, что ряд
(7)
сходится при .
Сначала покажем, что при , последовательные приближения принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.
Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.
Далее, по индукции, поскольку принадлежат интервалу , то и
.
Отсюда
.
Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7), применяя условие Липшица.
Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):
;
(8.2) .
Для третьего члена применяем, аналогично, условие Липшица и оценку (8.2):
;
(8.3) .
Далее применим метод индукции. Пусть
(8.n) .
Тогда
;
(8.n+1) .
Итак, поскольку (8.n) справедливо для и из (8.n) следует (8.n+1), то (8.n) выполняется для любых .
Запишем ряд (7) в виде:
(7.1) ,
где .
Применим (8.n) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.1) ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.1), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.1) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.1) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .
2) Доказательство того, что Y является решением (4)
Рассмотрим уравнение (5.n):
(5.n) .
Докажем, что при , это уравнение стремится к уравнению
(11) .
В силу (10) левая часть уравнения (5.n) стремится к .
Теперь покажем, что
.
Перепишем правую часть (5.n):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.
Оценим абсолютную величину последнего члена:
.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
.
Тогда
.
Поскольку произвольно, то
Поэтому
.
То есть при уравнение
(5.n)
принимает вид
(11) .
Доказательство единственности решения
Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Будем считать, что . В противном случае поменяем местами и .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.
Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .
Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .
Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).
Сделаем оценку, применяя уравнение (4) и условие Липшица:
;
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.
Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов. Опубликовано: Изменено:
