Дифференциальные уравнения с разделяющимися переменными
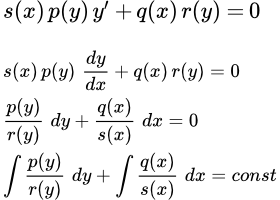
Определение
Пусть s(x), q(x) – функции от переменной x;
p(y), r(y) – функции от переменной y.
- Дифференциальное уравнение с разделяющимися переменными
- – это уравнение вида
Метод решения дифференциального уравнения с разделяющимися переменными
Рассмотрим уравнение:
(i) .
Выразим производную y′ через дифференциалы.
;
.
Умножим на dx.
(ii)
Разделим уравнение на s(x) r(y). Это можно сделать, если s(x) r(y) ≠ 0. При s(x) r(y) ≠ 0 имеем
.
Интегрируя, получаем общий интеграл в квадратурах
(iii) .
Поскольку мы делили на s(x) r(y), то получили интеграл уравнения при s(x) ≠ 0 и r(y) ≠ 0. Далее нужно решить уравнение
r(y) = 0.
Если это уравнение имеют корни, то они также являются решениями уравнения (i). Пусть уравнение r(y) = 0. имеет n корней ai, r(ai) = 0, i = 1, 2, ... , n. Тогда постоянные y = ai являются решениями уравнения (i). Часть этих решений может уже содержаться в общем интеграле (iii).
Заметим, что если исходное уравнение задано в форме (ii), то следует также решить уравнение
s(x) = 0.
Его корни bj, s(bj) = 0, j = 1, 2, ... , m. дают решения x = bj.
Пример решения дифференциального уравнения с разделяющимися переменными
Решить уравнение
Решение
Выразим производную через дифференциалы:
Умножим на dx и разделим на . При y ≠ 0 имеем:
Интегрируем.
Вычисляем интегралы, применяя формулу .
Подставляя, получаем общий интеграл уравнения
.
Теперь рассмотрим случай, y = 0.
Очевидно, что y = 0 является решением исходного уравнения. Оно не входит в общий интеграл .
Поэтому добавим его в окончательный результат.
Ответ
; y = 0.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
