Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными
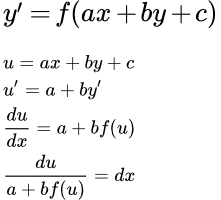
Постановка задачи
Рассмотрим дифференциальное уравнение
(i) ,
где f – функция, a, b, c – постоянные, b ≠ 0.
Это уравнение приводится к уравнению с разделяющимися переменными.
Метод решения
Делаем подстановку:
u = ax + by + c
Здесь y – функция от переменной x. Поэтому u – тоже функция от переменной x.
Дифференцируем по x
u′ = (ax + by + c)′ = a + by′
Подставляем (i)
u′ = a + by′ = a +b f(ax + by + c) = a + b f(u)
Или:
(ii)
Разделяем переменные. Умножаем на dx и делим на a + b f(u). Если a + b f(u) ≠ 0, то
Интегрируя, мы получаем общий интеграл исходного уравнения (i) в квадратурах:
(iii) .
В заключении рассмотрим случай
(iv) a + b f(u) = 0.
Предположим, что это уравнение имеет n корней u = ri, a + b f(ri) = 0, i = 1, 2, ... n. Поскольку функция u = ri является постоянной, то ее производная по x равна нулю. Поэтому u = ri является решением уравнения (ii).
Однако, уравнение (ii) не совпадает с исходным уравнением (i) и, возможно, не все решения u = ri, выраженные через переменные x и y, удовлетворяют исходному уравнению (i).
Таким образом, решением исходного уравнения является общий интеграл (iii) и некоторые корни уравнения (iv).
Пример решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными
Решить уравнение
(1)
Решение
Делаем подстановку:
u = x – y
Дифференцируем по x и выполняем преобразования:
;
Умножаем на dx и делим на u2.
Если u ≠ 0, то получаем:
Интегрируем:
Применяем формулу из таблицы интегралов:
Вычисляем интеграл
Тогда
;
, или
Общее решение:
.
Теперь рассмотрим случай u = 0, или u = x – y = 0, или
y = x.
Поскольку y′ = (x)′ = 1, то y = x является решением исходного уравнения (1).
Ответ
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
