Теорема существования и единственности решения системы дифференциальных уравнений
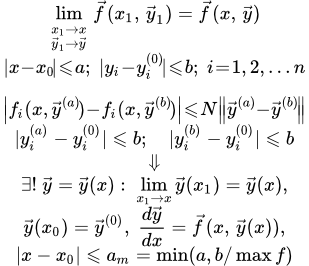
Здесь мы рассматриваем теорему существования и единственности решения системы дифференциальных уравнений с неизвестными функциями от переменной :
(1.1) ;
(1.2) ;
...
(1.n) .
Формулировка и доказательство этой теоремы является непосредственным обобщением теоремы для уравнения первого порядка, которое рассмотрено на странице “Теорема существования и единственности решения ДУ первого порядка”.
Векторная форма записи
Поскольку уравнения (1.1) – (1.n) однотипны, то мы применим векторную форму записи. Это позволит сократить объем выкладок и сделает доказательство более ясным.
Совокупность неизвестных функций мы будем обозначать одним вектором . Совокупность функций от независимой переменной и от зависимых функций мы обозначим как
.
То есть совокупность из величин мы будем обозначать вектором . Равенство
будет обозначать систему из уравнений:
,
где .
Под нормой вектора мы будем понимать сумму модулей его компонент:
.
Формулировка теоремы
Пусть дана система дифференциальных уравнений:
(1)
с начальными условиями
(1.0) .
Пусть – непрерывных функций от переменных в замкнутой области :
и, следовательно, ограничены некоторым положительным значением :
(2) .
И пусть функции удовлетворяют в области условию Липшица:
(3) ,
где – положительное число.
Тогда существует единственное решение системы (1):
,
удовлетворяющее начальным условиям , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .
Условие Липшица
Условие Липшица имеет вид:
(3) .
или в развернутом виде:
(3.1) ,
где – положительное число;
, и – любые значения из области .
Если условие Липшица выполняется и в некоторой точке существует частная производная , то она ограничена по модулю значением .
Для доказательства положим в (3.1) для всех . Тогда (3.1) примет вид:
.
Перейдем к пределу :
.
Если в области функции имеют непрерывные частные производные , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частные производные непрерывны в замкнутой области, то они ограничены:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой компоненты принадлежат интервалам между и :
.
Тогда:
.
Доказательство существования решения
Приведем исходную систему (1) с начальными условиями (1.0) к системе интегральных уравнений. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем каждое уравнение по от до :
;
Подставим начальные условия . В результате получим систему интегральных уравнений:
(4) .
Покажем, что система интегральных уравнений (4) эквивалентна дифференциальным уравнениям (1) с начальными условиями (1.0). Для этого нужно показать, что из (1) и (1.0) следует (4) и из (4) следует (1) и (1.0). То, что из (1) и (1.0) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.0). Для этого подставим в (4) . Получим начальные условия (1.0). Продифференцировав обе части системы (4) по , получаем (1).
Далее мы пытаемся найти решение уравнений (4) с помощью последовательных приближений. Для этого определяем ряд векторов функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.........
(5.m) .
Функции непрерывны, потому что интеграл есть непрерывная функция от верхнего предела. Мы предполагаем, что при , стремится к решению системы (4):
(6) ,
где – решение системы (4). Если мы докажем это, то мы докажем существование решения.
Доказательство существования решения будем проводить в два этапа:
1} вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет системе (4):
.
1) Доказательство существования предела y(m) при m стремящемся к бесконечности
Сведем последовательные приближения (5.1) – (5.m) к суммам рядов. Для этого пишем:
.
Таким образом нам нужно доказать, что ряды
(7)
сходятся при .
Сначала покажем, что при , компоненты последовательных приближений принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.
Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.
Далее, по индукции, поскольку принадлежит интервалу , то и
.
Отсюда
.
Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7).
Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):
;
(8.2) .
Далее применим метод индукции. Пусть
(8.m) .
Тогда
;
(8.m+1) .
Итак, поскольку (8.m) справедливо для и из (8.m) следует (8.m+1), то (8.m) выполняется для любых .
Запишем -й ряд (7) в виде:
(7.i) ,
где .
Применим (8.m) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.i), кроме первого, ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.i), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.i) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.i) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .
2) Доказательство того, что Y является решением (4)
Рассмотрим уравнение (5.m):
(5.m) .
Докажем, что при , это уравнение стремится к уравнению
(11) .
В силу (10) левая часть уравнения (5.m) стремится к .
Теперь покажем, что
.
Перепишем правую часть (5.m):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.
Оценим абсолютную величину последнего члена:
.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
(12) .
Пусть есть наибольшее из чисел . Тогда (12) выполняется для всех и для всех .
Тогда
.
Поскольку произвольно, то
Поэтому
.
То есть при уравнение
(5.m) .
принимает вид
(11) .
Доказательство единственности решения
Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Тогда .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.
Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .
Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .
Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).
Сделаем оценку, применяя уравнение (4) и условие Липшица:
.
Итак, мы получили оценку:
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.
Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов. Опубликовано:
