Теорема существования и единственности решения дифференциального уравнения произвольного порядка
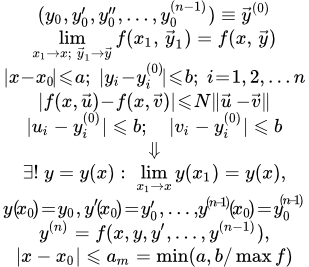
Здесь мы рассмотрим теорему существования и единственности решения дифференциального уравнения (ДУ) произвольного порядка. Для доказательства теоремы мы сведем ДУ к системе ДУ первого порядка и воспользуемся результатом теоремы существования и единственности решения системы дифференциальных уравнений.
Формулировка теоремы
Пусть дано дифференциальное уравнение n-го порядка:
(1)
с начальными условиями при :
(2) , , , ... , ,
где – некоторые числа (постоянные).
Пусть – непрерывная функция от переменных в замкнутой области :
; ; ; ; ... ;
и, следовательно, ограничена, по абсолютной величине, некоторым положительным значением :
(3) .
Здесь и есть некоторые положительные числа.
И пусть функция удовлетворяет в области условию Липшица:
(4) ,
где – положительное число;
; ; ; ... ; ;
; ; ; ... ; .
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальным условиям (2), определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .
Доказательство теоремы
Приведение к системе дифференциальных уравнений
Для доказательства, приведем уравнение
(1)
к системе дифференциальных уравнений первого порядка. Для этого вводим вспомогательных функций от переменной :
.
Свяжем их соотношениями:
; ; ; ... .
Дифференцируя уравнение по , находим:
;
.
Дифференцируя еще раз, имеем:
;
.
Таким образом
.
При имеем:
.
Дифференцируем по :
.
Тогда исходное уравнение (1) можно представить в виде системы дифференциальных уравнений первого порядка:
(5.1) ;
(5.2) ;
(5.3) ;
...
(5.n) ,
с начальными условиями:
(6) , , , ... , .
Применение теоремы единственности и существования для системы дифференциальных уравнений
Теперь воспользуемся результатом теоремы существования и единственности решения системы дифференциальных уравнений.
В нашем случае
;
;
...
;
.
Для удобства переобозначим переменные.
;
;
...
;
.
Все функции непрерывны по своим аргументам. непрерывна по условию теоремы. Остальные функции зависят только от одного из аргументов и являются линейными функциями. Поэтому они тоже непрерывны.
Все функции удовлетворяют условию Липшица. удовлетворяет условию Липшица по условию теоремы. Частные производные остальных функций либо равны нулю ( при ), либо равны единице ( при ). Поэтому частные производные непрерывны. Из этого следует, что функции удовлетворяют условию Липшица. Доказательство этого утверждения приведено в разделе “Условие Липшица”.
Итак, все условия теоремы существования и единственности решения системы ДУ выполнены. Поэтому решение системы (5) с начальными условиями (6) существует и единственно. И, следовательно, решение дифференциального уравнения (1) с начальными условиями (2) также существует и единственно.
Теорема доказана.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов. Опубликовано:
