Решение двойственной задачи
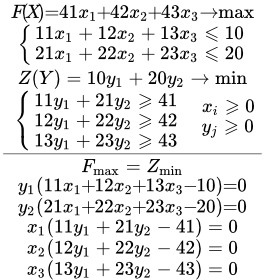
Здесь мы рассмотрим вопрос, как из решения прямой задачи, получить решение двойственной задачи.
Теоремы двойственности
Первая теорема двойственности
Если одна из пары двойственных задач имеет оптимальное решение,то и двойственная задача имеет оптимальное решение. При этом значения целевых функций прямой и двойственной задачи, для оптимальных решений, равны друг другу.
Если одна из пары двойственных задач не имеет решения вследствие неограниченности целевой функции,
то двойственная задача не имеет решения вследствие несовместимости системы ограничений.
Вторая теорема двойственности
Пусть мы имеем симметричную пару двойственных задач (1) и (2):(1.1) ;
(1.2)
(2.1) ;
(2.2)
Для того чтобы допустимые решения и являлись оптимальными решениями двойственных задач (1) и (2),
необходимо и достаточно, чтобы выполнялись следующие равенства:
(3) , ;
(4) , .
Для наглядности, выпишем равенства (3) и (4) в развернутом виде:
(3.1)
(3.2)
(3.m)
(4.1)
(4.2)
(4.n)
Метод решения двойственной задачи
Применяя теоремы двойственности, можно получить решение двойственной задачи из решения прямой. Опишем метод решения двойственной задачи.
Пусть мы нашли решение прямой задачи (1) с оптимальным значением целевой функции и с оптимальным планом . Подставим найденные значения в систему ограничений (1.2). Тогда если -е неравенство не является равенством, то есть если
,
то, согласно (3.i),
.
Рассматривая все строки системы ограничений (1.2), мы найдем, что часть переменных двойственной задачи равна нулю.
Далее замечаем, что если , то, согласно (4.k), -я строка системы ограничений (2.2) является равенством:
.
Составив все строки системы ограничений (2.2), для которых , мы получим систему уравнений, из которой можно найти ненулевые значения переменных .
На основании первой теоремы двойственности, минимальное значение целевой функции
.
Если известно решение задачи (2), то аналогичным образом можно найти решение задачи (1).
Примеры решения двойственной задачи из решения прямой
Пример 1
Пусть дана задача линейного программирования:
;
Известно решение этой задачи:
; .
Составить двойственную задачу и получить ее решение из решения прямой.
Решение
Составляем двойственную задачу.
;
Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.
Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи.
(П1.1.1) ;
(П1.1.2) ;
(П1.1.3) ;
(П1.1.4) .
Поскольку первая и четвертая строки являются строгими неравенствами (не являются равенствами), то
и .
Поскольку и , то 2-я и 4-я строки двойственной задачи являются равенствами:
Подставим уже найденные значения и , имеем:
Отсюда
;
; .
Ответ
Двойственная задача имеет вид:
;
Ее решение
;
Пример 2
Дана задача линейного программирования:
(П2.1.1) ;
(П2.1.2)
Найти решение этой задачи, решив двойственную задачу графическим методом.
Решение
Составляем двойственную задачу.
(П2.2.1) ;
(П2.2.2)
Решение задачи (П2.2) приводится на странице “Решение задач линейного программирования графическим методом”. Решение задачи (П2.2) имеет вид:
; .
Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.
Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи (П2.2).
;
;
.
Поскольку третья строка является строгим неравенством (не являются равенством), то
.
Поскольку и , то 1-я и 2-я строки двойственной задачи (П2.1) являются равенствами:
Подставим найденное значение .
Решаем систему уравнений.
;
;
;
; ;
.
Ответ
Решение исходной задачи (П2.1) имеет вид:
; .
Автор: Олег Одинцов. Опубликовано:
