Лемма о вложенных отрезках (принцип Коши – Кантора)
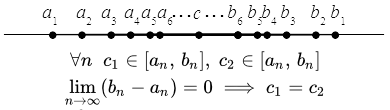
Определение вложенных отрезков
Пусть a и b – два действительных числа (a ∈ R, b ∈ R). И пусть a < b . Множество чисел x , удовлетворяющих неравенствам a ≤ x ≤ b , называется отрезком с концами a и b . Отрезок обозначается так: [a, b ] .
- Вложенные отрезки
- Последовательность числовых отрезков
(1) [a1 , b1 ], [a2 , b2 ], ... , [an , bn ], ...; an ∈ R, bn ∈ R, n = 1, 2, 3, ...
называется последовательностью вложенных отрезков, если каждый последующий отрезок содержится в предыдущем:
[a1 , b1 ] ⊃ [a2 , b2 ] ⊃ ... ⊃ [an , bn ] ⊃ ... .
То есть концы отрезков связаны неравенствами:
a1 ≤ a2 ≤ ... ≤ an ≤ ... ≤ bn ≤ ... ≤ b2 ≤ b1 .
Лемма о вложенных отрезках (принцип Коши – Кантора)
Для любой последовательности вложенных отрезков (1)существует точка c ∈ R , принадлежащая всем этим отрезкам.
Если длины отрезков стремятся к нулю:
limn → ∞ (bn – an ) = 0 ,
то такая точка единственная.
Эту лемму также называют теоремой о вложенных отрезках или принципом Коши – Кантора.
Доказательство
Доказательство первой части леммы
Последовательности {an } и {bn } монотонны и ограничены. Поэтому по теореме Вейерштрасса о пределе монотонной последовательности, они имеют пределы
(1) ca = limn → ∞ an , cb = limn → ∞ bn .
Причем для всех n
(2) an ≤ ca , bn ≥ cb .
Возможны три варианта.
1. ca < cb
2. ca = cb
3. ca > cb
1. При ca < cb , в силу (2), любая точка c : ca ≤ c ≤ cb принадлежит всем отрезкам [an , bn ] .
2. При ca = cb , также в силу (2), точка c = ca = cb принадлежит всем отрезкам [an , bn ] .
3. Докажем, что третьего случая не существует. Предположим противное. Пусть ca > cb . Возьмем произвольную точку c , принадлежащую интервалу (cb , ca ) : cb < c < ca . Согластно определению предела последовательности, в силу (1), существует такое число N , так что для всех n > N , выполняются неравенства:
| an – ca | < | ca – c | ; | bn – cb | < | cb – c | .
Воспользуемся тем, что an ≤ ca , c < ca , cb ≤ bn , cb < c . Тогда в этих неравенствах можно раскрыть знаки модуля:
ca – an < ca – c; bn – cb < c – cb .
Отсюда c < an , bn < c , или
bn < an ,
что противоречит условию вложенности an ≤ bn .
Доказательство второй части леммы
Пусть limn → ∞ (bn – an ) = 0 . В соответствии с определением предела последовательности, это означает, что для любого положительного числа ε > 0 существует такое натуральное число N , зависящее от ε , что для всех натуральных n > N выполняется неравенство
(3) | bn – an | < ε .
Допустим противное. Пусть существует две различные точки c1 и c2 , c1 ≠ c2 , принадлежащие всем отрезкам. Это означает, что для всех n выполняются следующие неравенства:
an ≤ c1 ≤ bn ;
an ≤ c2 ≤ bn .
Отсюда
| c1 – c2 | ≤ bn – an .
Применяя (3) имеем:
| c1 – c2 | ≤ ε .
Это неравенство должно выполняться для любых положительных значений ε . Отсюда следует, что
c1 = c2 .
Лемма доказана.
Замечания
1. Существование точки, принадлежащей всем отрезкам, вытекает из определения действительного числа, как предела последовательности рациональных чисел. То есть ca и cb являются действительными числами, и могут быть иррациональными. Поэтому к множеству рациональных чисел, лемма о вложенных отрезках не применима.
Например, мы могли бы выбрать отрезки так, чтобы и левые и правые концы сходились к иррациональному числу √ 2 . Тогда любое рациональное число, при увеличении n , всегда выпадало бы из системы отрезков. Единственное число, которое принадлежит всем отрезком – это иррациональное число √ 2 .
2. Первую часть леммы можно доказать другим способом, воспользовавшись аксиомой полноты действительных чисел.
Аксиома полноты действительных чисел заключается в следующем. Пусть множества A и B есть два подмножества действительных чисел R , таких что для любых двух элементов a ∈ A и b ∈ B этих множеств выполняется неравенство a ≤ b . Тогда существует такое действительное число c , что для всех a ∈ A и b ∈ B выполняются неравенства:
a ≤ c ≤ b .
Применим эту аксиому. Пусть множество A есть множество левых концов отрезков, а множество B – правых. Тогда между двумя любыми элементами этих множеств выполняется неравенство an ≤ bm . Тогда из аксиомы полноты действительных чисел следует, что существует такое число c , что для всех n выполняются неравенства:
an ≤ c ≤ bn .
Оно и означает, что точка c принадлежит всем отрезкам.
Использованная литература:
О.В. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Автор: Олег Одинцов. Опубликовано: Изменено: