Бесконечно удаленные точки и их свойства

Приводятся определения бесконечно удаленных точек – бесконечности без знака, плюс и минус бесконечности. Дается определение расширенной числовой прямой. Представлены свойства бесконечно удаленных точек и рассмотрен вопрос о доказательстве этих свойств. Приводятся примеры неопределенных операций.

Содержание

См. также:

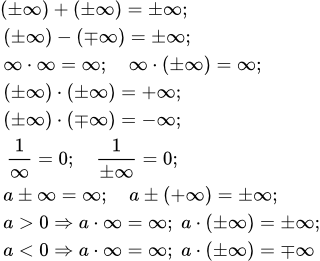
Определения бесконечно удаленных точек

Если некоторая последовательность сходится к конечному числу a, то пишут
.
Ранее мы ввели в рассмотрение бесконечно большие последовательности. Мы приняли, что они являются сходящимися и обозначили их пределы символами и . Эти символы обозначают бесконечно удаленные точки. Они не принадлежат множеству действительных чисел. Но понятие предела позволяет ввести такие точки и дает инструмент для изучения их свойств с помощью действительных чисел.

Бесконечно удаленная точка,: или бесконечность без знака, – это предел, к которому стремится любая бесконечно большая последовательность.
Бесконечно удаленная точка плюс бесконечность,: – это предел, к которому стремится любая бесконечно большая последовательность с положительными членами.
Бесконечно удаленная точка минус бесконечность,: – это предел, к которому стремится любая бесконечно большая последовательность с отрицательными членами.

Для любого действительного числа a имеют место следующие неравенства:
;
.

Используя действительные числа, мы ввели понятие окрестности бесконечно удаленной точки.
Окрестностью точки является множество .
Окрестностью точки является множество .
Наконец, окрестностью точки является множество .
Здесь M – произвольное, сколь угодно большое действительные число.

Таким образом, мы расширили множество действительных чисел, введя в него новые элементы. В связи с этим, имеет место следующее определение.

Расширенной числовой прямой: или расширенным множеством действительных чисел называется множество действительных чисел , дополненное элементами и :
.

Вначале мы выпишем свойства, которыми обладают точки и . Далее рассмотрим вопрос строгого математического определения операций для этих точек и доказательства этих свойств.

Свойства бесконечно удаленных точек

Сумма и разность.
; ;
; ;

Произведение и частное.
; ; ;
;
;
; ; .

Связь с действительными числами.
Пусть a – произвольное действительное число. Тогда
; ;
; ; ; .
Пусть a > 0. Тогда
; ; .
Пусть a < 0. Тогда
; .

Неопределенные операции.
; ; ; ;
; ; ;
; ;
.

Доказательство свойств бесконечно удаленных точек

Определение математических операций

Мы уже дали определения для бесконечно удаленных точек. Теперь мы должны определить для них математические операции. Поскольку мы определили эти точки посредством последовательностей, то и операции с этими точками также следует определить, используя последовательности.

Суммой двух точек, принадлежащих расширенному множеству действительных чисел: c = a + b, ,
мы будем называть предел
,
где и – произвольные последовательности, имеющие пределы
и .

Аналогичным образом определяются операции вычитания, умножения и деления. Только, в случае деления, элементы в знаменателе дроби не должны быть равными нулю.
Тогда разность двух точек:
– это предел .
Произведение точек:
– это предел .
Частное:
– это предел .
Здесь и – произвольные последовательности, чьи пределы равны a и b, соответственно. В последнем случае, .

Доказательство свойств

Для доказательства свойств бесконечно удаленных точек, нам нужно использовать свойства бесконечно больших последовательностей.

Рассмотрим свойство:
.
Для его доказательства, мы должны показать, что
,
где и – произвольные последовательности, с пределами и .

Другими словами нам нужно доказать, что сумма двух произвольных последовательностей, сходящихся к плюс бесконечности, сходится к плюс бесконечности.

Докажем это. Поскольку и , то имеются некоторые функции и , так что для любого положительного числа M₁ выполняются неравенства:
;
.
Тогда при и имеем:
.
Положим . Тогда
при ,
где .
Это и означает, что .

Аналогичным способом доказываются и другие свойства. В качестве примера приведем еще одно доказательство.

Докажем, что:
.
Для этого мы должны показать, что
,
где и – произвольные последовательности, с пределами и .

То есть нам нужно доказать, что произведение двух бесконечно больших последовательностей является бесконечно большой последовательностью.

Неопределенные операции

Часть математических операций с бесконечно удаленными точками не определены. Чтобы показать их неопределенность, нужно привести пару частных случаев, когда результат операции зависит от выбора входящих в них последовательностей.

Рассмотрим такую операцию:
.
Легко показать, что если и , то предел суммы последовательностей зависит от выбора последовательностей и .

Действительно, возьмем . Пределы этих последовательностей равны . Предел суммы

равен бесконечности.

Теперь возьмем . Пределы этих последовательностей также равны . Но предел их суммы

равен нулю.

То есть при условии, что и , значение предела суммы может принимать различные значения. Поэтому операция не определена.

Аналогичным способом можно показать неопределенность остальных операции, представленных выше.

Автор: Олег Одинцов. Опубликовано: 19-09-2017

См. также: