Определение конечного предела последовательности

Приводится определение конечного предела последовательности. Рассмотрены связанные с этим свойства и эквивалентное определение. Приводится определение, что точка a не является пределом последовательности. Рассмотрены примеры, в которых доказывается существование предела, используя определение.

Содержание

См. также:

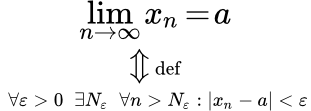
Здесь мы рассмотрим определение конечного предела последовательности. Случай последовательности, сходящейся к бесконечности, рассмотрен на странице «Определение бесконечно большой последовательности».

Определение предела последовательности

Предел последовательности: – это такое число a , если для любого положительного числа ε > 0 существует такое натуральное число N_ε , зависящее от ε , что для всех натуральных n > N_ε выполняется неравенство
|x_n – a| < ε .
Здесь x_n – элемент последовательности с номером n . Предел последовательности обозначается так:
a = lim_{n → ∞} x_n .
Или x_n → a при n → ∞ .

Преобразуем неравенство:
| x_n – a | < ε ;
– ε < x_n – a < ε ;
a – ε < x_n < a + ε .

ε - окрестность точки a: – это открытый интервал (a – ε, a + ε).

Сходящаяся последовательность: – это последовательность, у которой существует предел a = lim_{n → ∞} x_n . Также говорят, что последовательность {x_n } сходится к a .

Расходящаяся последовательность: – это последовательность, не имеющая предела.

Из определения следует, что, если последовательность имеет предел a , то какую бы ε - окрестностью точки a мы не выбрали, за ее пределами может оказаться, лишь конечное число элементов последовательности, или вообще ни одного (пустое множество). А любая ε - окрестность содержит бесконечное число элементов. В самом деле, задав определенное число ε , мы, тем самым имеем число N_ε . Так что все элементы последовательности с номерами n > N_ε , по определению, находятся в ε - окрестностью точки a . Первые N_ε элементов могут находиться где угодно. То есть за пределами ε - окрестности может находиться не более N_ε элементов – то есть конечное число.

Также заметим, что разность | x_n – a | вовсе не обязана монотонно стремиться к нулю, то есть все время убывать. Она может стремиться к нулю не монотонно: может то возрастать, то убывать, имея локальные максимумы. Однако эти максимумы, с ростом n , должны стремиться к нулю (возможно тоже не монотонно).

С помощью логических символов существования и всеобщности, определение предела можно записать следующим образом:
(1) lim_{n → ∞} x_n = a ^def⇐⇒ ∀ε > 0 ∃N_ε ∀n > N_ε : | x_n – a | < ε .

Определение, что число a не является пределом

Теперь рассмотрим обратное утверждение, что число a не является пределом последовательности.

Число a не является пределом последовательности {x_n } , если существует такое ε > 0 , что для любого натурального n существует такое натуральное m > n , что
| x_m – a | ≥ ε .

Запишем это утверждение с помощью логических символов.
(2) lim_{n → ∞} x_n ≠ a ⇔ ∃ε > 0 ∀n ∃m > n : | x_m – a | ≥ ε .

Утверждение, что число a не является пределом последовательности, означает, что
можно выбрать такую ε - окрестность точки a , за пределами которой будет находиться бесконечное число элементов последовательности.

Рассмотрим пример. Пусть задана последовательность {x_n } с общим элементом
(3)

x_n = {

1n ,

если n четно ast 1n + 2,

если n нечетно

Любая окрестность точки x = 0 содержит бесконечное число элементов. Однако эта точка не является пределом последовательности, поскольку и любая окрестность точки x = 2 также содержит бесконечное число элементов. Возьмем ε - окрестность точки x = 0 с ε = 1 . Это будет интервал ( –1, +1) . Все элементы, кроме первого, с четными n принадлежат этому интервалу. Но все элементы с нечетными n находятся за пределами этого интервала, поскольку они удовлетворяют неравенству x_n > 2 . Поскольку число нечетных элементов бесконечно, то за пределами выбранной окрестности будет находиться бесконечное число элементов. Поэтому точка x = 0 не является пределом последовательности.

Теперь покажем это, строго придерживаясь утверждения (2). Точка a = 0 не является пределом последовательности (3), поскольку существует такое ε = 1 , так что, для любого натурального n , существует нечетное m > n , для которого выполняется неравенство
| x_m – 0 | ≥ 1 .

Также можно показать, что любая точка a не может являться пределом этой последовательности. Мы всегда можем выбрать такую ε - окрестность точки a , которая не содержит либо точку 0, либо точку 2. И тогда за пределами выбранной окрестности будет находиться бесконечное число элементов последовательности.

Эквивалентное определение предела последовательности

Можно дать эквивалентное определение предела последовательности, если расширить понятие ε - окрестности. Мы получим равносильное определение, если в нем, вместо ε - окрестности, будет фигурировать любая окрестность точки a .

Окрестности точки: – это любой открытый интервал, содержащий эту точку. Математически окрестность точки определяется так: (a – ε₁ , a + ε₂ ) , где ε₁ и ε₂ – произвольные положительные числа.

Тогда эквивалентное определение предела будет следующим.

Предел последовательности: – это такое число a , если для любой его окрестности существует такое натуральное число N , так что все элементы последовательности x_n с номерами n > N принадлежат этой окрестности.

Это определение можно представить и в развернутом виде.

Предел последовательности: – это такое число a , если для любых положительных чисел ε₁ > 0 и ε₂ > 0 существует такое натуральное число N , зависящее от ε₁ и ε₂ , что для всех натуральных n > N выполняются неравенства
a – ε₁ < x_n < a + ε₂ .

Доказательство равносильности определений

Докажем, что, представленные выше, два определения предела последовательности равносильны.

Пусть число a является пределом последовательности {x_n } согласно первому определению. Это означает, что имеется функция N(ε ) , так что для любого положительного числа ε выполняются неравенства:
(4) – ε < x_n – a < ε при n > N(ε ) .

Покажем, что число a является пределом последовательности и по второму определению. То есть нам нужно показать, что существует такая функция N^′(ε₁ , ε₂ ) , так что для любых положительных чисел ε₁ и ε₂ выполняются неравенства:
(5) – ε₁ < x_n – a < ε₂ при n > N^′(ε₁ , ε₂ ) .

Пусть мы имеем два положительных числа: ε₁ и ε₂ . И пусть ε – наименьшее из них: ε = min (ε₁ , ε₂ ) . Тогда ε ≤ ε₁ ; ε ≤ ε₁ ; – ε ≥ – ε₁ . Используем это в (5):
– ε₁ ≤ – ε < x_n – a < ε ≤ ε₂ .
Но неравенства – ε < x_n – a < ε выполняются при n > N(ε ) . Тогда и неравенства (5) выполняются при n > N(ε ) .

То есть мы нашли такую функцию N^′(ε₁ , ε₂ ) = N(min (ε₁ , ε₂ )) , при которой выполняются неравенства (5) для любых положительных чисел ε₁ и ε₂ .
Первая часть доказана.
Теперь пусть число a является пределом последовательности {x_n } согласно второму определению. Это означает, что имеется функция N^′(ε₁ , ε₂ ) , так что для любых положительных чисел ε₁ и ε₂ выполняются неравенства:
(5) – ε₁ < x_n – a < ε₂ при n > N^′(ε₁ , ε₂ ) .

Покажем, что число a является пределом последовательности и по первому определению. Для этого нужно положить ε₁ = ε₂ = ε . Тогда при n > N^′(ε, ε ) выполняются неравенства:
– ε < x_n – a < ε .
Это соответствует первому определению с N(ε ) = N^′(ε, ε ) .
Равносильность определений доказана.

Примеры

Все примеры Здесь мы рассмотрим несколько примеров, в которых требуется доказать, что заданное число a является пределом последовательности. При этом нужно задать произвольные положительное число ε и определить функцию N от ε такую, что для всех n > N выполняется неравенство | x_n – a | < ε .

Доказать, что lim_{n → ∞} (– 1 )ⁿn = 0 ⇓, lim_{n → ∞} nn² + 1 = 0 ⇓, lim_{n → ∞} 3n² + n + 12n² – 1 = 32 ⇓, lim_{n → ∞} 3n² + n + 12n² – 1 = 32 ⇓.

Пример 1

Все примеры ⇑ Доказать, что lim_{n → ∞} (– 1 )ⁿn = 0 .

Решение

Выпишем определение предела последовательности:
(1) lim_{n → ∞} x_n = a ^def⇐⇒ ∀ε > 0 ∃N_ε ∀n > N_ε : | x_n – a | < ε .
В нашем случае x_n = (– 1 )ⁿn , a = 0 ;
| x_n – a | = | (– 1 )ⁿn – 0 | = | (– 1 )ⁿn | = 1n .

Вводим положительные числа N_ε и ε :
| x_n – a | = 1n < 1N_ε ≤ ε .
Воспользуемся свойствами неравенств. Тогда если N_ε ≥ 1ε и n > N_ε , то
| x_n – a | < ε .

То есть, для любого положительного ε > 0 , мы можем взять любое натуральное число, большее или равное 1 / ε :
N_ε ≥ 1ε .
Тогда
| x_n – a | < ε при n > N_ε .
Это означает, что число a = 0 является пределом заданной последовательности:
lim_{n → ∞} x_n = a .

Ответ

N_ε ≥ 1ε

Пример 2

Все примеры ⇑ С помощью определения предела последовательности доказать, что
lim_{n → ∞} nn² + 1 = 0 .

Решение

Выпишем определение предела последовательности:
(1) lim_{n → ∞} x_n = a ^def⇐⇒ ∀ε > 0 ∃N_ε ∀n > N_ε : | x_n – a | < ε .
В нашем случае x_n = nn² + 1 , a = 0 ;
| x_n – a | = | nn² + 1 – 0 | = nn² + 1 < nn² = 1n .

Вводим положительные числа N_ε и ε :
| x_n – a | < 1n < 1N_ε ≤ ε .
Воспользуемся свойствами неравенств. Тогда если N_ε ≥ 1ε и n > N_ε , то
| x_n – a | < ε .

То есть, для любого положительного ε > 0 , мы можем взять любое натуральное число, большее или равное 1 / ε :
N_ε ≥ 1ε .
Тогда
| x_n – a | < ε при n > N_ε .
Это означает, что число a = 0 является пределом последовательности {x_n } :
lim_{n → ∞} x_n = a .

Ответ

N ≥ 1ε

Пример 3

Все примеры ⇑ Используя определение предела последовательности доказать, что
lim_{n → ∞} 3n² + n + 12n² – 1 = 32 .

Решение

Вводим обозначения x_n = 3n² + n + 12n² – 1 , a = 32 .
Преобразуем разность:
x_n – a = 3n² + n + 12n² – 1 – 32 = 2(3n² + n + 1 )2(2n² – 1 ) – 3(2n² – 1 )2(2n² – 1 ) = 2n + 54n² – 2 .
Для натуральных n = 1, 2, 3, ... имеем:
| x_n – a | = | 2n + 54n² – 2 | = 2n + 54n² – 2 ≤ 2n + 5n4n² – 2n² = 72n .

Выпишем определение предела последовательности:
(1) lim_{n → ∞} x_n = a ^def⇐⇒ ∀ε > 0 ∃N_ε ∀n > N_ε : | x_n – a | < ε .
Вводим положительные числа N_ε и ε :
| x_n – a | ≤ 72n < 72N_ε ≤ ε .
Тогда если N_ε ≥ 72ε и n > N_ε , то
| x_n – a | < ε .

То есть, для любого положительного ε > 0 , мы можем взять любое натуральное число, большее или равное 72ε :
N_ε ≥ 72ε .
При этом
| x_n – a | < ε при n > N_ε .
Это означает, что число a = 3 / 2 является пределом последовательности {x_n } :
lim_{n → ∞} x_n = a .

Ответ

N_ε ≥ 72ε .

Пример 4

Все примеры ⇑ Используя определение предела последовательности доказать, что
lim_{n → ∞} sin n√ n = 0 .

Решение

Выпишем определение предела последовательности:
(1) lim_{n → ∞} x_n = a ^def⇐⇒ ∀ε > 0 ∃N_ε ∀n > N_ε : | x_n – a | < ε .
В нашем случае x_n = sin n√ n , a = 0 ;
| x_n – a | = | sin n√ n – 0 | = | sin n | √ n ≤ 1√ n .

Вводим положительные числа N_ε и ε :
| x_n – a | ≤ 1√ n < 1√ N_ε ≤ ε .
Тогда если N_ε ≥ 1ε² и n > N_ε , то
| x_n – a | < ε .

То есть, для любого положительного ε > 0 , мы можем взять любое натуральное число, большее или равное 1 / ε² :
N_ε ≥ 1ε² .
Тогда
| x_n – a | < ε при n > N_ε .
Это означает, что число a = 0 является пределом последовательности {x_n } :
lim_{n → ∞} x_n = a .

Ответ

N_ε ≥ 1ε²

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 12-07-2017 Изменено: 08-12-2017

См. также: