Основные свойства конечных пределов последовательностей
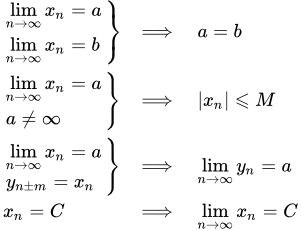
Свойства и теоремы
Свойство окрестности сходящейся последовательности
Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Доказательство ⇓
Свойство окрестности последовательности, не сходящейся к числу a
Если число a не является пределом последовательности , то существует такая окрестность точки a, за пределами которой находится бесконечное число элементов последовательности.
Доказательство ⇓
Теорема единственности предела числовой последовательности
Если последовательность имеет предел, то он единственный.
Доказательство ⇓
Теорема об ограниченности последовательности, имеющей конечный предел
Если последовательность имеет конечный предел, то она ограничена.
Доказательство ⇓
Теорема о пределе постоянной последовательности
Если каждый элемент последовательности равен одному и тому же числу C: , то эта последовательность имеет предел, и этот предел равен числу C.
Доказательство ⇓
Влияние конечного числа элементов на сходимость
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Доказательство ⇓
Доказательство свойств и теорем
При доказательстве свойств, мы будем использовать определение предела последовательности:
.
Свойство окрестности сходящейся последовательности
Все свойства ⇑ Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Доказательство
-
Пусть точка a является пределом последовательности . Согласно определению предела последовательности это означает, что для любой окрестности точки a существует такое натуральное число N, что все элементы последовательности с номерами принадлежат этой окрестности. (см. «Эквивалентное определение предела последовательности»).
Тогда первые N элементов последовательности могут находиться где угодно. То есть за пределами окрестность могут находиться не более N элементов последовательности – конечное число или пустое множество.
Первая часть доказана.
-
Пусть теперь за пределами любой окрестности точки a находится конечное число элементов последовательности или пустое множество. Пусть N есть наибольший номер элемента, находящегося за пределами окрестности. Тогда все элементы последовательности с номерами принадлежат этой окрестности. Это означает, что точка a является пределом последовательности.
Свойство доказано.
Свойство окрестности последовательности, не сходящейся к числу a
Все свойства ⇑ Если число a не является пределом последовательности , то существует такая окрестность точки a, за пределами которой находится бесконечное число элементов последовательности.
Доказательство
Допустим противное. Пусть число a не является пределом последовательности и за пределами любой окрестности точки a находится только конечное число элементов последовательности. Рассмотрим произвольную окрестность точки a. Пусть N есть наибольший номер элемента, находящегося за ее пределами. Тогда все элементы с номерами принадлежат окрестности. Но это означает, что число a является пределом последовательности, что противоречит предположению.
Свойство доказано.
Теорема единственности предела числовой последовательности
Все свойства ⇑ Если последовательность имеет предел, то он единственный.
Доказательство
Предположим противное, что у последовательности существует два различных предела:
и . Причем .
Поскольку, по предположению, существует предел , то это означает, что имеется функция . Так что при , для любого , выполняется неравенство . То есть элементы последовательности, при , находятся в интервале
(1.1) .
Точно также, поскольку существует предел , то имеется функция . Так что при , для любого , выполняется неравенство . Тогда при , элементы последовательности находятся в интервале
(1.2) .
Возьмем . То есть ε равно половине длины отрезка ab. При таком выборе, интервалы (1.1) и (1.2) не имеют общих точек.
Пусть N – наибольшее из чисел и . Тогда для всех , должны выполняться соотношения (1.1) и (1.2). То есть элементы последовательности, при , должны находиться и в интервале (1.1) и в интервале (1.2). Возникает противоречие, поскольку эти интервалы не имеют общих точек.
Теорема доказана.
Мы взяли . Для доказательства можно было взять другие значения и , для которых интервалы (1.1) и (1.2) не имеют общих точек.
Теорема об ограниченности последовательности, имеющей конечный предел
Все свойства ⇑ Если последовательность имеет конечный предел, то она ограничена.
Доказательство
Пусть последовательность имеет конечный предел a:
.
Это означает, что имеется функция такая, что при , для любого , выполняется неравенство
(2.1) .
Возьмем любое значение ε. Например, . Тогда, в силу (2.1), элементы последовательности с номерами , находятся в пределах интервала
(2.2) .
Элементы последовательности, с номерами , могут находиться за пределами интервала (2.2). Но их конечное число. Поэтому их значения ограничены некоторыми числами и . То есть, при , элементы последовательности ограничены интервалом
(2.3) .
В качестве и можно взять значения наименьшего и наибольшего элемента при .
Итак, при , элементы последовательности ограничены неравенствами (2.3), а при – неравенствами (2.2). Тогда для любого n, выполняются следующие неравенства:
(2.4) ,
где есть наименьшее из чисел и ; – наибольшее из чисел и .
Неравенства (2.4) означают, что последовательность ограничена снизу значением , и сверху – значением , или просто ограничена. Что и требовалось доказать.
Теорема доказана.
Также ограниченность элементов можно записать одним неравенством:
,
где M есть наибольшее из чисел и .
Теорема о пределе постоянной последовательности
Все свойства ⇑ Если каждый элемент последовательности равен одному и тому же числу C: , то эта последовательность имеет предел, и этот предел равен числу C.
Доказательство
В случае последовательности с равными элементами, какую бы ε - окрестность точки C мы не взяли, все элементы этой последовательности будут находиться в этой окрестности:
.
Действительно, подставив сюда , имеем:
;
,
что выполняется для всех n, поскольку .
Тогда в качестве функции мы можем взять любую постоянную, не зависящую от ε, например .
Тогда для любого положительного числа существует такое число , что для всех натуральных выполняется неравенство
.
Это и означает, что число C является пределом последовательности .
Влияние конечного числа элементов на сходимость
Все свойства ⇑ Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Доказательство
Хотя здесь мы рассматриваем только конечные пределы, но доказательство этой теоремы повторяется один в один, если включить в рассмотрение и бесконечные пределы. Поэтому рядом с формулами, применимыми только для конечных пределов, мы будем приводить универсальные формулы, пригодные как для конечных, так и для бесконечных пределов. Их мы будем помечать звездочкой. При первом чтении раздела их можно пропустить.
Пусть мы имеем последовательность , которая имеет конечный предел
.
Это означает, что имеется такая функция , что для любого , элементы последовательности с номерами , находятся в ε - окрестности числа a:
(3.1) .
В более общем случае, когда a может быть также одной из бесконечно удаленных точек: или , вместо (3.1) следует записать следующее:
(3.1*) ,
где обозначает ε – окрестность точки a.
Рассмотрим последовательность , которая получается из , добавлением первых m элементов. То есть
(3.2)
и есть произвольные числа при .
Покажем, что . Для этого нам нужно найти такую функцию , что для любого , элементы последовательности с номерами , находятся в интервале:
(3.3) ;
(3.3*) .
Подставим в (3.1) и прибавим к обеим частям второго неравенства m:
;
* .
Заменим n + m на k:
;
* .
Эти неравенства совпадают с (3.3), если положить и обозначить индекс k буквой n. Поэтому число a является пределом последовательности .
Теперь рассмотрим последовательность , которая получается из , удалением первых m элементов. То есть
(3.4) .
Покажем, что . То есть нам нужно найти такую функцию , что для любого , элементы последовательности с номерами , находятся в интервале
(3.5) ;
(3.5*) .
Для этого преобразуем неравенства (3.1). Заметим, что функция определена не однозначно. Ее всегда можно увеличить на любое натуральное число. То есть вместо (3.1) можно записать так:
(3.1.1) ;
(3.1.1*) .
Действительно, поскольку , то из неравенства следует неравенство .
Подставим в (3.1.1) n = k + m:
;
* .
Подставим (3.4) и преобразуем:
;
* .
Эти неравенства совпадают с (3.5), если положить и обозначить индекс k буквой n. Поэтому число a является пределом последовательности .
Итак, мы доказали, что если число a является пределом последовательности при , то число a также является пределом расширенной последовательности и усеченной последовательности .
Пусть теперь число a не является пределом последовательности . Докажем, что это число также не является пределом последовательности . Допустим противное, что число a является пределом последовательности . Но последовательность получается из последовательности удалением первых элементов. Поэтому, как мы только что доказали, последовательность должна иметь предел a. Возникает противоречие. Поэтому число a не может быть пределом последовательности . Точно так же, если число a не является пределом последовательности , то оно не является и пределом последовательности .
Тем самым мы доказали, что добавление или удаление первых элементов не влияет на сходимость последовательности. Докажем, что изменение первых m элементов также не влияет на сходимость. Для доказательства удалим первые m элементов у исходной последовательности. Получим промежуточную последовательность, сходимость которой такая же, как у исходной. Затем добавим в промежуточную последовательность первые m элементов с произвольными значениями. Получим последовательность, у которой, по отношению к исходной, изменены первые m элементов. Сходимость такой последовательности такая же как и у промежуточной, а поэтому такая же как и у исходной.
Свойство доказано.
Автор: Олег Одинцов. Опубликовано: Изменено:
