Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′
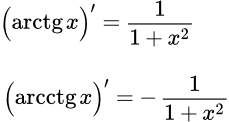
Производная по переменной x от арктангенса x равна единице, деленной на один плюс x в квадрате:
.
Производная по переменной x от арккотангенса x равна минус производной от арктангенса. То есть она равна минус единице, деленной на один плюс x в квадрате:
.
Вывод производной арктангенса
Здесь мы полагаем, что нам известна производная тангенса:
.
Далее мы выводим формулу производной арктангенса, учитывая, что арктангенс является функцией, обратной к тангенсу.
По формуле производной обратной функции
Рассмотрим функцию арктангенс:
y = arctg x.
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от – π/2 до + π/2:
.
Арктангенс является функцией, обратной к тангенсу:
x = tg y.
Для определения его производной, применим формулу производной обратной функции:
(1) .
Производная тангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arctg x;
x = tg y.
Теперь выразим правую часть формулы (2) через переменную x. Для этого воспользуемся формулой и выполним преобразования:
.
Отсюда
.
Подставим в (2):
.
Тем самым мы вывели формулу производной арктангенса:
.
Второй способ
Поскольку арктангенс и тангенс являются взаимно обратными функциями, то
(3) .
Продифференцируем это уравнение по переменной x. То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .
Из таблицы производных имеем:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.
Подставим в (4):
.
Отсюда
.
Вывод производной арккотангенса
Используя связь между арктангенсом и арккотангенсом
Производную арккотангенса можно получить из производной арктангенса, если воспользоваться связью между арктангенсом и арккотангенсом:
.
Отсюда
.
По формуле производной обратной функции
Рассмотрим функцию арккотангенс:
y = arcctg x.
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от 0 до π:
.
Арккотангенс является функцией, обратной к котангенсу:
x = ctg y.
Для определения его производной, применим формулу производной обратной функции:
(1) .
Считаем, что производная котангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arcctg x;
x = ctg y.
Выразим правую часть формулы (5) через переменную x. Для этого выполним преобразования:
.
Отсюда
.
Подставим в (5):
.
Таким образом, мы вывели формулу производной арккотангенса:
.
Второй способ
Поскольку арккотангенс и котангенс являются взаимно обратными функциями, то
(6) .
Продифференцируем это уравнение по переменной x:
(7) .
Из таблицы производных находим:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.
Подставим в (7):
.
Отсюда
.
Автор: Олег Одинцов. Опубликовано:
