Основные элементарные функции и их свойства

Раздел содержит справочный материал по основным элементарным функциям и их свойствам. Приводится классификация элементарных функций. Ниже даны ссылки на подразделы, в которых рассматриваются свойства конкретных функций - графики, формулы, производные, первообразные (интегралы), разложения в ряды, выражения через комплексные переменные.

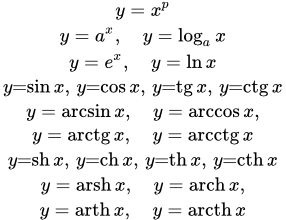
Страницы со справочным материалом по элементарным функциям

Классификация элементарных функций

Алгебраическая функция – это функция, которая удовлетворяет уравнению:
,
где – многочлен от зависимой переменной y и независимой переменной x. Его можно записать в виде:
,
где – многочлены.

Алгебраические функции делятся на многочлены (целые рациональные функции), рациональные функции и иррациональные функции.

Целая рациональная функция, которая также называется многочленом или полиномом, получается из переменной x и конечного числа чисел с помощью арифметических действий сложения (вычитания) и умножения. После раскрытия скобок, многочлен приводится к каноническому виду:
.

Дробно-рациональная функция, или просто рациональная функция, получается из переменной x и конечного числа чисел с помощью арифметических действий сложения (вычитания), умножения и деления. Рациональную функцию можно привести к виду
,
где и – многочлены.

Иррациональная функция – это алгебраическая функция, не являющаяся рациональной. Как правило, под иррациональной функцией понимают корни и их композиции с рациональными функциями. Корень степени n определяется как решение уравнения
.
Он обозначается так:
.

Трансцендентными функциями называются неалгебраические функции. Это показательные, тригонометрические, гиперболические и обратные к ним функции.

Обзор основных элементарных функций

Все элементарные функции можно представить в виде конечного числа операций сложения, вычитания, умножения и деления, произведенных над выражением вида:
z ^t.
Обратные функции могут выражаться также через логарифмы. Ниже перечислены основные элементарные функции.

Степенная функция:
y(x) = x ^p,
где p - показатель степени. Она зависит от основания степени x.
Обратной к степенной функции является также степенная функция:
.
При целом неотрицательном значении показателя p она является многочленом. При целом значении p – рациональной функцией. При рациональном значении – иррациональной функцией.

Трансцендентные функции

Показательная функция:
y(x) = a ^x,
где a - основание степени. Она зависит от показателя степени x.
Обратная функция - логарифм по основанию a:
x = log _a y.

Экспонента, е в степени х:
y(x) = e ^x,
Это показательная функция, производная которой равна самой функции:
.
Основанием степени экспоненты является число e:
≈ 2,718281828459045....
Обратная функция - натуральный логарифм - логарифм по основанию числа e:
x = ln y ≡ log _e y.

Тригонометрические функции:
Синус:   ;
Косинус:   ;
Тангенс:   ;
Котангенс:   ;
Здесь i - мнимая единица, i ² = –1.

Обратные тригонометрические функции:
Арксинус:   x = arcsin y,   ;
Арккосинус:   x = arccos y,   ;
Арктангенс:   x = arctg y,   ;
Арккотангенс:   x = arcctg y,   .

Гиперболические функции:
Гиперболический синус:   ;
Гиперболический косинус:   ;
Гиперболический тангенс:   ;
Гиперболический котангенс:   .

Обратные гиперболические функции:
Ареасинус:   ;
Ареакосинус:   ;
Ареатангенс:   ;
Ареакотангенс:   .