Обратные гиперболические функции, их графики и формулы
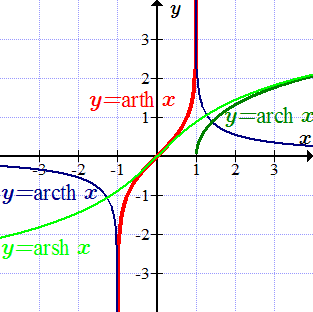
Определения обратных гиперболических функций, их области определений и значений
arsh x - обратный гиперболический синус
- Обратный гиперболический синус (ареасинус)
- – это функция , обратная к гиперболическому синусу x = sh y, имеющая область определения –∞ < x < +∞ и множество значений –∞ < y < +∞.
Ареасинус строго возрастает на всей числовой оси.
arch x - обратный гиперболический косинус
- Обратный гиперболический косинус (ареакосинус)
- – это функция , обратная к гиперболическому косинусу x = сh y, имеющая область определения 1 ≤ x < +∞ и множество значений 0 ≤ y < +∞.
Ареакосинус строго возрастает на своей области определения.
Вторая ветвь ареакосинуса также определена при x ≥ 1 и расположена симметрично относительно оси абсцисс, – ∞ < y ≤ 0 :
. Она строго убывает на области определения.
arth x - обратный гиперболический тангенс
- Обратный гиперболический тангенс (ареатангенс)
- – это функция , обратная к гиперболическому тангенсу x = th y, имеющая область определения – 1 < x < 1 и множество значений –∞ < y < +∞.
Ареатангенс строго возрастает на своей области определения.
arcth x - обратный гиперболический котангенс
- Обратный гиперболический котангенс (ареакотангенс),
- – это функция , обратная к гиперболическому котангенсу x = cth y, имеющая область определения |x| > 1 и множество значений y ≠ 0.
Ареакотангенс строго убывает на своей области определения.
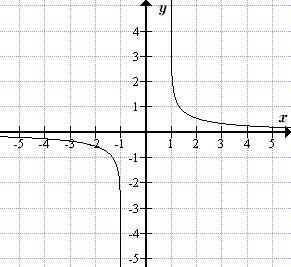
Графики обратных гиперболических функций
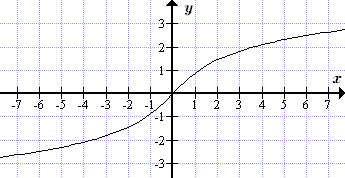
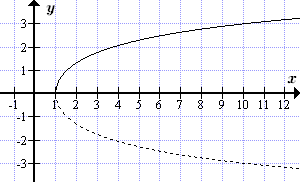
Пунктиром показана вторая ветвь ареакосинуса.
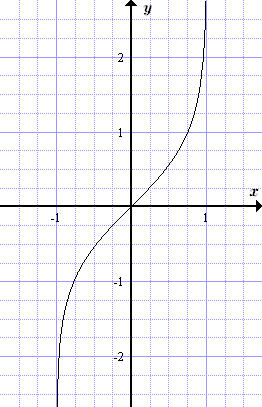
Формулы с обратными гиперболическими функциями
Связь с тригонометрическими функциями
Arsh iz = i Arcsin z; Arch z = i Arccos z;
Arcsin iz = i Arsh z; Arccos z = – i Arch z;
Arth iz = i Arctg z; Arcth iz = – i Arcctg z;
Arctg iz = i Arth z; Arcctg iz = – i Arcth z;
Здесь i – мнимая единица, i2 = –1.
Четность
arsh(–x) = – arsh x; arch(–x) ≠ ± arch x;
arth(–x) = – arth x; arcth(–x) = – arcth x.
Функции arsh(x), arth(x), arcth(x) – нечетные. Функция arch(x) – не является четной или нечетной.
Формулы связи обратных гиперболических синусов через тангенсы и косинусов через котангенсы
;
;
;
.
Формулы суммы и разности
;
;
;
.
Производные обратных гиперболических функций
;
.
Интегралы от arsh x, arch x, arth x, arcth x
arsh x
Для вычисления интеграла от гиперболического арксинуса, делаем подстановку x = sh t и интегрируем по частям:
.
arch x
Аналогично, для гиперболического арккосинуса. Делаем подстановку x = ch t и интегрируем по частям учитывая, что t ≥ 0:
.
arth x
Делаем подстановку x = th t и интегрируем по частям:
;
;
;
.
arcth x
Аналогично получаем:
.
Разложения в ряды
arsh x
При |x| < 1 имеет место следующее разложение:
arth x
При |x| < 1 имеет место следующее разложение:
arcth x
При |x| > 1 имеет место следующее разложение:
Обратные функции
Гиперболический синус
При – ∞ < y < ∞ и – ∞ < x < ∞ имеют место формулы:
,
.
Гиперболический косинус
При 1 ≤ y < ∞ и 0 ≤ x < ∞ имеют место формулы:
,
.
Гиперболический тангенс
При – 1 < y < 1 и – ∞ < x < ∞ имеют место формулы:
,
.
Гиперболический котангенс
При – ∞ < y < – 1 или 1 < y < ∞ и x ≠ 0 имеют место формулы:
,
.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано:
