Решение кубических уравнений
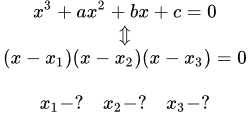
Здесь мы рассматриваем решение кубических уравнений вида
(1) x 3 + ax 2 + bx + c = 0 .
Далее считаем, что a, b, c – это действительные числа.
Если исходное уравнение имеет вид:
(2) αx 3 + βx 2 + γx + δ = 0 ,
то разделив его на α , получаем уравнение вида (1) с коэффициентами
a = βα , b = γα , c = δα .
Уравнение (1) имеет три корня: x1 , x2 и x3 . Один из корней всегда действительный. Действительный корень мы обозначаем как x1 . Корни x2 и x3 могут быть либо действительными, либо комплексно сопряженными. Действительные корни могут быть кратными. Например, если x2 = x3 ≠ x1 , то x2 и x3 – это двукратные корни (или корни кратности 2), а x1 – простой корень.
Если известен один корень
Пусть нам известен один корень кубического уравнения (1). Обозначим известный корень как x1 . Тогда разделив уравнение (1) на x – x1 , получим квадратное уравнение. Решая квадратное уравнение, найдем еще два корня x2 и x3 .
Для доказательства воспользуемся тем, что кубический многочлен можно представить в виде:
x 3 + ax 2 + bx + c = (x – x1 )(x – x2 )(x – x3 ) .
Тогда, разделив (1) на x – x1 , получаем квадратное уравнение.
Примеры деления многочленов представлены на странице
“Деление многочленов уголком”.
Решение квадратных уравнений рассмотрено на странице
“Корни квадратного уравнения”.
Если один из корней – целый
Если исходное уравнение имеет вид:
(2) αx 3 + βx 2 + γx + δ = 0 ,
и его коэффициенты α , β , γ , δ – целые числа, то можно попытаться найти целый корень. Если это уравнение имеет целый корень, то он является делителем коэффициента δ . Метод поиска целых корней заключается в том, что мы находим все делители числа δ и проверяем, выполняется ли для них уравнение (2). Если уравнение (2) выполняется, то мы нашли его корень. Обозначим его как x1 . Далее делим уравнение (2) на x – x1 . Получаем квадратное уравнение. Решая его, находим еще два корня.
Примеры определения целых корней даны на странице
Примеры разложения многочленов на множители > > >.
Поиск рациональных корней
Если в уравнении (2) α , β , γ , δ – целые числа, причем α ≠ 1 , и целых корней нет, то можно попытаться найти рациональные корни, то есть корни вида xi = mn , где m и n – целые.
Для этого умножим уравнение (2) на α 2 и сделаем подстановку y = αx :
α 3 x 3 + βα 2 x 2 + γα 2 x + α 2 δ = 0 ;
(3) y 3 + βy 2 + αγy + α 2 δ = 0 .
Далее ищем целые корни уравнения (3) среди делителей свободного члена α 2 δ .
Если мы нашли целый корень y1 уравнения (3), то, возвращаясь к переменной x , получаем рациональный корень уравнения (2):
x1 = y1 α .
Формулы Кардано и Виета для решения кубического уравнения
Если нам не известен ни один корень, и целых корней нет, то найти корни кубического уравнения можно по формулам Кардано.
Рассмотрим кубическое уравнение:
(1) x 3 + ax 2 + bx + c = 0 .
Сделаем подстановку:
x = y – a3 .
После этого уравнение приводится к неполному или приведенному виду:
(4) y 3 + py + q = 0 ,
где
(5) p = – a 2 3 + b ; q = 2( a3 ) 3 – ab3 + c .
Формула Кардано для неполного (приведенного) кубического уравнения имеет вид:
y = u + v ;
u = 3 √ – q2 + √ Q ;
v = 3 √ – q2 – √ Q ;
uv = – p3 ;
Q = ( p3 ) 3 + ( q2 ) 2 .
По формуле Кардано, мы находим три корня величины u . Затем, используя формулу uv = – p3 , находим значения величины v .
После разделения кубических корней величины u , формула Кардано принимает следующий вид:
(6) y1 = A + B , y2,3 = – A + B2 ± i A – B2 √ 3 ,
где
(7) A = 3 √ – q2 + √ Q ; B = 3 √ – q2 – √ Q ; AB = – p3 ;
(8) Q = ( p3 ) 3 + ( q2 ) 2 .
При Q > 0 , для A и B нужно выбирать действительные корни, которые автоматически связаны соотношением AB = – p3 . При этом мы получим одно действительное решение y1 и два комплексно сопряженных y2 и y3 .
При Q = 0 имеем:
A = B ; y1 = 2A ; y2 = y3 = A .
В этом случае мы имеем два кратных действительных корня. Если A = 0 , то мы имеем три кратных корня.
При Q < 0 мы имеем три действительных корня. При этом A и B – комплексные. Поэтому решение приводится к тригонометрической форме, которая имеет название формулы Виета:
(9) y1 = 2 √ – p3 cos (φ / 3 ) ;
(10) y2,3 = 2 √ – p3 cos (φ / 3 ± 2π / 3 ) ,
где
(11) cos φ = – q2 ( 3– p ) 3 / 2 ; 0 ≤ φ ≤ π .
Примеры решений по формулам Кардано и Виета
Решить кубические уравнения:
x 3 + 2x 2 + x + 1 = 0 ;
x 3 – 2x 2 – x + 1 = 0 .
Решение примеров > > >
Онлайн калькулятор > > >
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.
Автор: Олег Одинцов. Опубликовано: Изменено: