Формула Кардано для решения кубического уравнения
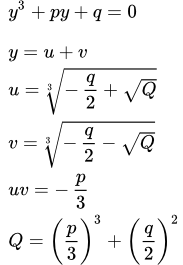
Сведение кубического уравнения к приведенному виду
Рассмотрим кубическое уравнение:
(1) ,
где . Разделим его на :
(2) ,
где , , .
Далее считаем, что , и – есть действительные числа.
Приведем уравнение (2) к более простому виду. Для этого сделаем подстановку
.
;
;
.
Приравняем коэффициент при к нулю. Для этого положим
:
;
;
.
Получаем уравнение приведенного вида:
(3) ,
где
(4) ; .
Вывод формулы Кардано
Решаем уравнение (3). Делаем подстановку
(5) :
;
;
;
.
Чтобы это уравнение удовлетворялось, положим
(6) ;
(7) .
Из (7) имеем:
.
Подставим в (6):
;
.
Решаем квадратное уравнение.
(8) .
Возьмем верхний знак “+”:
,
где мы ввели обозначение
.
Из (6) имеем:
.
Итак, мы нашли решение приведенного уравнения в следующем виде:
(5) ;
(9) ;
(10) ;
(7) ;
(11) .
Такое решение называется формулой Кардано.
Если мы, при выборе знака квадратного корня в (8), возьмем нижний знак, то и поменяются местами и мы не получим ничего нового. Величины и равны кубическим корням, поэтому они имеют по три значения. Из всех возможных пар и нужно выбрать такие, которые удовлетворяют уравнению (7).
Итак, алгоритм решения приведенного кубического уравнения
(3)
следующий.
1) Вначале мы определяем любое значение квадратного корня .
2) Вычисляем три значения кубического корня .
3) Используя формулу (7), для каждого значения , вычисляем значение :
.
В результате получаем три пары величин и .
4) Для каждой пары величин и , по формуле (5) находим значения корней приведенного уравнения (3).
5) Рассчитываем значения корней исходного уравнения (1) по формуле
.
Таким способом мы получаем значения трех корней исходного уравнения. При два или три корня являются кратными (равными).
На шаге 3) данного алгоритма можно поступить по другому. Мы можем вычислить три значения величины по формуле (10). И далее составить три пары корней и так, чтобы для каждой пары выполнялось соотношение
(7) .
Случай Q ≥ 0
Рассмотрим случай . При этом и являются действительными числами. Введем обозначения. Пусть и обозначают действительные значения кубических корней.
Найдем остальные значения корней и . Запишем и в следующем виде:
; ,
где – есть целое число;
– мнимая единица, .
Тогда
.
Присваивая значения , получаем три корня:
, ;
, ;
, .
Точно также получаем три корня :
;
;
.
Теперь группируем и в пары, чтобы, для каждой пары выполнялось соотношение
(7) .
Поскольку , то
.
Тогда
.
Отсюда получаем первую пару: .
Далее замечаем, что
.
Поэтому
; .
Тогда и являются еще двумя парами.
Теперь получаем три корня приведенного уравнения:
;
;
.
Их также можно записать в следующем виде:
(12) ; .
Эти формулы называются формулой Кардано.
При , . Два корня являются кратными:
; .
При все три корня являются кратными:
.
Случай Q < 0
Если мы проследим вывод формулы (12), то увидим, что весь вывод сохранит силу и при отрицательном значении . То есть и могут быть комплексными. Тогда для и можно выбрать любые значения кубических корней, между которыми выполняется соотношение
.
Формула Кардано для решения кубического уравнения
Итак, мы установили, что корни приведенного кубического уравнения
можно найти по формуле Кардано:
, ,
где
; ; ;
.
Однако, при , формула Виета являются более удобной.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
