Теорема Виета для квадратных и других уравнений
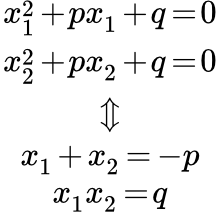
Квадратные уравнения
Теорема Виета
Пусть и обозначают корни приведенного квадратного уравнения
(1) .
Тогда сумма корней равна коэффициенту при , взятому с обратным знаком. Произведение корней равно свободному члену:
;
.
Замечание по поводу кратных корней
Если дискриминант уравнения (1) равен нулю, то это уравнение имеет один корень. Но, чтобы избежать громоздких формулировок, принято считать, что в этом случае, уравнение (1) имеет два кратных, или равных, корня:
.
Доказательство первое
Найдем корни уравнения (1). Для этого применим формулу для корней квадратного уравнения:
;
;
.
Находим сумму корней:
.
Чтобы найти произведение, применим формулу:
.
Тогда
.
Теорема доказана.
Доказательство второе
Если числа и являются корнями квадратного уравнения (1), то
.
Раскрываем скобки.
.
Таким образом, уравнение (1) примет вид:
.
Сравнивая с (1) находим:
;
.
Теорема доказана.
Обратная теорема Виета
Пусть и есть произвольные числа. Тогда и являются корнями квадратного уравнения
,
где
(2) ;
(3) .
Доказательство обратной теоремы Виета
Рассмотрим квадратное уравнение
(1) .
Нам нужно доказать, что если и , то и являются корнями уравнения (1).
Подставим (2) и (3) в (1):
.
Группируем члены левой части уравнения:
;
;
(4) .
Подставим в (4) :
;
.
Уравнение выполняется. То есть число является корнем уравнения (1).
Подставим в (4) :
;
.
Уравнение выполняется. То есть число является корнем уравнения (1).
Теорема доказана.
Теорема Виета для полного квадратного уравнения
Теперь рассмотрим полное квадратное уравнение
(5) ,
где , и есть некоторые числа. Причем .
Разделим уравнение (5) на :
.
То есть мы получили приведенное уравнение
,
где ; .
Тогда теорема Виета для полного квадратного уравнения имеет следующий вид.
Пусть и обозначают корни полного квадратного уравнения
.
Тогда сумма и произведение корней определяются по формулам:
;
.
Теорема Виета для кубического уравнения
Аналогичным образом мы можем установить связи между корнями кубического уравнения. Рассмотрим кубическое уравнение
(6) ,
где , , , есть некоторые числа. Причем .
Разделим это уравнение на :
(7) ,
где , , .
Пусть , , есть корни уравнения (7) (и уравнения (6)). Тогда
.
Сравнивая с уравнением (7) находим:
;
;
.
Теорема Виета для уравнения n-й степени
Тем же способом можно найти связи между корнями , , ... , , для уравнения n-й степени
.
Теорема Виета для уравнения n-й степени имеет следующий вид:
;
;
;
.
Чтобы получить эти формулы мы записываем уравнение в следующем виде:
.
Затем приравниваем коэффициенты при , , , ... , и сравниваем свободный член.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
С.М. Никольский, М.К. Потапов и др., Алгебра: учебник для 8 класса общеобразовательных учреждений, Москва, Просвещение, 2006.
Автор: Олег Одинцов. Опубликовано:
