Степенная функция, ее свойства и графики
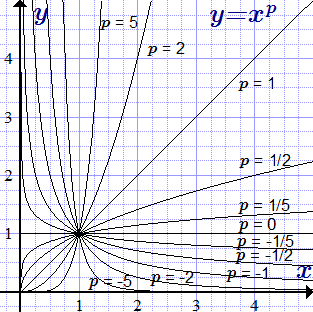
Формулы со степенной функцией
На области определения степенной функции y = x p имеют место следующие формулы:
; ;
;
; ;
; ;
; .
Свойства степенных функций и их графики
Далее мы рассматриваем степенную функцию
y(x) = x p .
Степенная функция с показателем равным нулю, p = 0
Если показатель степенной функции y = x p равен нулю, p = 0, то степенная функция определена для всех x ≠ 0 и является постоянной, равной единице:
y = x p = x 0 = 1, x ≠ 0 .
Степенная функция с натуральным нечетным показателем, p = n = 1, 3, 5, ...
Рассмотрим степенную функцию y = x p = x n с натуральным нечетным показателем степени n = 1, 3, 5, .... Такой показатель также можно записать в виде: n = 2k + 1, где k = 0, 1, 2, 3, ... – целое не отрицательное. Ниже представлены свойства и графики таких функций.

Область определения: –∞ < x < ∞
Множество значений: –∞ < y < ∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ < x < 0 выпукла вверх
при 0 < x < ∞ выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1,
y(–1) = (–1) n ≡ (–1) 2k+1 = –1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 1, функция является обратной к самой себе: x = y
при n ≠ 1, обратной функцией является корень степени n:
Степенная функция с натуральным четным показателем, p = n = 2, 4, 6, ...
Рассмотрим степенную функцию y = x p = x n с натуральным четным показателем степени n = 2, 4, 6, .... Такой показатель также можно записать в виде: n = 2k, где k = 1, 2, 3, ... – натуральное. Свойства и графики таких функций даны ниже.

Область определения: –∞ < x < ∞
Множество значений: 0 ≤ y < ∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x ≤ 0 монотонно убывает
при x ≥ 0 монотонно возрастает
Экстремумы: минимум, x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = (–1) n ≡ (–1) 2k = 1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 2, квадратный корень:
при n ≠ 2, корень степени n:
Степенная функция с целым отрицательным показателем, p = n = -1, -2, -3, ...
Рассмотрим степенную функцию y = x p = x n с целым отрицательным показателем степени n = -1, -2, -3, .... Если положить n = –k, где k = 1, 2, 3, ... – натуральное, то ее можно представить в виде:

Нечетный показатель, n = -1, -3, -5, ...
Ниже представлены свойства функции y = x n с нечетным отрицательным показателем n = -1, -3, -5, ....
Область определения: x ≠ 0
Множество значений: y ≠ 0
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно убывает
Экстремумы: нет
Выпуклость:
при x < 0: выпукла вверх
при x > 0: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак:
при x < 0, y < 0
при x > 0, y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = –1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –1,
при n < –2,
Четный показатель, n = -2, -4, -6, ...
Ниже представлены свойства функции y = x n с четным отрицательным показателем n = -2, -4, -6, ....
Область определения: x ≠ 0
Множество значений: y > 0
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0: монотонно возрастает
при x > 0: монотонно убывает
Экстремумы: нет
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак: y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = 1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –2,
при n < –2,
Степенная функция с рациональным (дробным) показателем
Рассмотрим степенную функцию y = x p с рациональным (дробным) показателем степени , где n – целое, m > 1 – натуральное. Причем, n, m не имеют общих делителей.
Знаменатель дробного показателя - нечетный
Пусть знаменатель дробного показателя степени нечетный: m = 3, 5, 7, ... . В этом случае, степенная функция x p определена как для положительных, так и для отрицательных значений аргумента x. Рассмотрим свойства таких степенных функций, когда показатель p находится в определенных пределах.
Показатель p отрицательный, p < 0
Пусть рациональный показатель степени (с нечетным знаменателем m = 3, 5, 7, ... ) меньше нуля: .

Нечетный числитель, n = -1, -3, -5, ...
Приводим свойства степенной функции y = x p с рациональным отрицательным показателем , где n = -1, -3, -5, ... - нечетное отрицательное целое, m = 3, 5, 7 ... - нечетное натуральное.
Область определения: x ≠ 0
Множество значений: y ≠ 0
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно убывает
Экстремумы: нет
Выпуклость:
при x < 0: выпукла вверх
при x > 0: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак:
при x < 0, y < 0
при x > 0, y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = –1
при x = 1, y(1) = 1 n = 1
Обратная функция:
Четный числитель, n = -2, -4, -6, ...
Свойства степенной функции y = x p с рациональным отрицательным показателем , где n = -2, -4, -6, ... - четное отрицательное целое, m = 3, 5, 7 ... - нечетное натуральное.
Область определения: x ≠ 0
Множество значений: y > 0
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0: монотонно возрастает
при x > 0: монотонно убывает
Экстремумы: нет
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак: y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = 1
при x = 1, y(1) = 1 n = 1
Обратная функция:
Показатель p положительный, меньше единицы, 0 < p < 1

Нечетный числитель, n = 1, 3, 5, ...
Представлены свойства степенной функции y = x p с рациональным показателем , находящимся в пределах 0 < p < 1, где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
Область определения: –∞ < x < +∞
Множество значений: –∞ < y < +∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при x < 0: выпукла вниз
при x > 0: выпукла вверх
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Знак:
при x < 0, y < 0
при x > 0, y > 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = –1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:
Четный числитель, n = 2, 4, 6, ...
Представлены свойства степенной функции y = x p с рациональным показателем , находящимся в пределах 0 < p < 1, где n = 2, 4, 6, ... – четное натуральное, m = 3, 5, 7 ... – нечетное натуральное.
Область определения: –∞ < x < +∞
Множество значений: 0 ≤ y < +∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0: монотонно убывает
при x > 0: монотонно возрастает
Экстремумы: минимум при x = 0, y = 0
Выпуклость: выпукла вверх при x ≠ 0
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Знак: при x ≠ 0, y > 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = 1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:
Показатель p больше единицы, p > 1

Нечетный числитель, n = 5, 7, 9, ...
Свойства степенной функции y = x p с рациональным показателем, большим единицы: . Где n = 5, 7, 9, ... – нечетное натуральное, m = 3, 5, 7 ... – нечетное натуральное.
Область определения: –∞ < x < ∞
Множество значений: –∞ < y < ∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ < x < 0 выпукла вверх
при 0 < x < ∞ выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = –1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:
Четный числитель, n = 4, 6, 8, ...
Свойства степенной функции y = x p с рациональным показателем, большим единицы: . Где n = 4, 6, 8, ... – четное натуральное, m = 3, 5, 7 ... – нечетное натуральное.
Область определения: –∞ < x < ∞
Множество значений: 0 ≤ y < ∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0 монотонно убывает
при x > 0 монотонно возрастает
Экстремумы: минимум при x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = 1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:
Знаменатель дробного показателя - четный
Пусть знаменатель дробного показателя степени четный: m = 2, 4, 6, ... . В этом случае, степенная функция x p не определена для отрицательных значений аргумента. Ее свойства совпадают со свойствами степенной функции с иррациональным показателем (см. следующий раздел).
Степенная функция с иррациональным показателем
Рассмотрим степенную функцию y = x p с иррациональным показателем степени p. Свойства таких функций отличаются от рассмотренных выше тем, что они не определены для отрицательных значений аргумента x. Для положительных значений аргумента, свойства зависят только от величины показателя степени p и не зависят от того, является ли p целым, рациональным или иррациональным.

Степенная функция с отрицательным показателем p < 0
Область определения: x > 0
Множество значений: y > 0
Монотонность: монотонно убывает
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Пределы: ;
Частное значение: При x = 1, y(1) = 1p = 1
Степенная функция с положительным показателем p > 0
Показатель меньше единицы 0 < p < 1
Область определения: x ≥ 0
Множество значений: y ≥ 0
Монотонность: монотонно возрастает
Выпуклость: выпукла вверх
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
Частные значения: При x = 0, y(0) = 0 p = 0.
При x = 1, y(1) = 1 p = 1
Показатель больше единицы p > 1
Область определения: x ≥ 0
Множество значений: y ≥ 0
Монотонность: монотонно возрастает
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
Частные значения: При x = 0, y(0) = 0 p = 0.
При x = 1, y(1) = 1 p = 1
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
