Методы вычисления неопределенных интегралов

Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций.

Содержание

См. также:

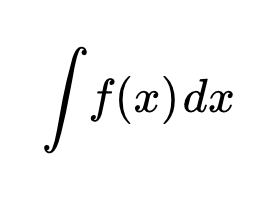
Первообразная и неопределенный интеграл

Первообразная F(x) от функции f(x) – это такая функция, производная которой равна f(x):
F′(x) = f(x), x ∈ Δ,
где Δ – промежуток, на котором выполняется данное уравнение.

Совокупность всех первообразных называется неопределенным интегралом:
,
где C – постоянная, не зависящая от переменной x.

Основные формулы и методы интегрирования

Таблица интегралов

Конечная цель вычисления неопределенных интегралов - путем преобразований, привести заданный интеграл к выражению, содержащему простейшие или табличные интегралы.
См. Таблица интегралов >>>

Правило интегрирования суммы (разности)

.
Здесь и далее u, v, w – функции от переменной x.

Вынесение постоянной за знак интеграла

Пусть c – постоянная, не зависящая от x. Тогда ее можно вынести за знак интеграла:

См. подробнее: Вычисление интегралов от многочленов >>>

Замена переменной

Пусть x – функция от переменной t, x = φ(t), тогда
.
Или наоборот, t = φ(x),
.

С помощью замены переменной можно не только вычислить простые интегралы, но и упростить вычисление более сложных.

См. подробнее: Интегрирование методом замены переменной >>>

Правило интегрирования по частям

См. подробнее: Метод интегрирования неопределенного интеграла по частям >>>

Интегрирование дробей (рациональных функций)

Введем обозначение. Пусть P_k(x), Q_m(x), R_n(x) обозначают многочлены степеней k, m, n, соответственно, относительно переменной x.

Рассмотрим интеграл, состоящий из дроби многочленов (так называемая рациональная функция):

Если k ≥ n, то сначала нужно выделить целую часть дроби:
.
Интеграл от многочлена S_k-n(x) вычисляется по таблице интегралов.

См. подробнее: Деление многочленов уголком >>>

Остается интеграл:
, где m < n.
Для его вычисления, подынтегральное выражение нужно разложить на простейшие дроби.

Для этого нужно найти корни уравнения:
Q_n(x) = 0.
Используя полученные корни, нужно представить знаменатель в виде произведения сомножителей:
Q_n(x) = s (x-a)^n_a (x-b)^n_b ... (x²+ex+f)^n_e (x²+gx+k)^n_g ... .
Здесь s – коэффициент при xⁿ, x² + ex + f > 0, x² + gx + k > 0, ... .

См. подробнее: Методы разложения многочленов на множители >>>
Примеры разложения многочленов на множители >>>

После этого разложить дробь на простейшие:

См. подробнее: Методы разложения рациональных дробей на простейшие >>>

Интегрируя, получаем выражение, состоящее из более простых интегралов.
Интегралы вида

приводятся к табличным подстановкой t = x – a.

Рассмотрим интеграл:

Преобразуем числитель:
.
Подставляя в подынтегральное выражение, получаем выражение, в которое входят два интеграла:
,
.
Первый, подстановкой t = x² + ex + f приводится к табличному.
Второй, по формуле приведения:

приводится к интегралу

Приведем его знаменатель к сумме квадратов:
.
Тогда подстановкой , интеграл

также приводится к табличному.

См. подробнее: Интегрирование простейших дробей >>>
Примеры интегрирования рациональных функций >>>

Интегрирование иррациональных функций

Введем обозначение. Пусть R( u₁, u₂, ... , u_n ) означает рациональную функцию от переменных u₁, u₂, ... , u_n. То есть
,
где P, Q – многочлены от переменных u₁, u₂, ... , u_n.

Дробно-линейная иррациональность

Рассмотрим интегралы вида:
,
где – рациональные числа, m₁, n₁, ..., m_s, n_s – целые числа.
Пусть n – общий знаменатель чисел r₁, ..., r_s.
Тогда интеграл сводится к интегралу от рациональных функций подстановкой:
.

См. подробнее: Интегрирование дробно-линейной иррациональности >>>

Интегралы от дифференциальных биномов

Рассмотрим интеграл:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.

1) Если p – целое. Подстановка x = t^N, где N – общий знаменатель дробей m и n.
2) Если – целое. Подстановка a xⁿ + b = t^M, где M – знаменатель числа p.
3) Если – целое. Подстановка a + b x^{– n} = t^M, где M – знаменатель числа p.

Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.

В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям m и p. Это можно сделать с помощью формул приведения:
;
.

См. подробнее: Интегрирование дифференциального бинома >>>

Интегралы, содержащие квадратный корень из квадратного трехчлена

Здесь мы рассматриваем интегралы вида:
,

Подстановки Эйлера

Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0;
, при c > 0;
, где x₁ – корень уравнения a x² + b x + c = 0. Если это уравнение имеет действительные корни.

См. подробнее: Подстановки Эйлера >>>

Тригонометрические и гиперболические подстановки

Также эти интегралы можно вычислить с помощью тригонометрических и гиперболических подстановок. В некоторых случаях этот способ вычисления интеграла является самым простым.
См. подробнее: Тригонометрические и гиперболические подстановки >>>

Прямые методы

В большинстве случаев, подстановки Эйлера приводят к более длинным вычислениям, чем прямые методы. С помощью прямых методов интеграл приводится к одному из перечисленных ниже видов.

I тип

Интеграл вида:
,
где P_n(x) – многочлен степени n.

Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:

Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты A_i.

См. подробнее: Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена >>>

II тип

Интеграл вида:
,
где P_m(x) – многочлен степени m.

Подстановкой t = (x – α)^–1 этот интеграл приводится к предыдущему типу. Если m ≥ n, то у дроби следует выделить целую часть.

См. подробнее: Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена >>>

III тип

Третий и наиболее сложный тип:
.

Здесь нужно сделать подстановку:
.
После чего интеграл примет вид:
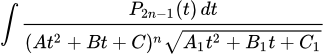$\int \frac{P_{2n-1}(t)\, dt}{(At^2+Bt+C)^n \sqrt{A_1 t^2+B_1 t+C_1}}$ .
Далее, постоянные α, β нужно выбрать такими, чтобы коэффициенты при t обратились в нуль:
B = 0, B₁ = 0.
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
z² = A₁t² + C₁;
y² = A₁ + C₁ t^–2.

См. подробнее: Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена >>>

Общий случай

Самый общий интеграл вида:
,
сводится к интегралам трех предыдущих типов. Для этого достаточно, уничтожая иррациональность в знаменателе, преобразовать подынтегральную функцию к виду:
φ(x) + ψ(x)y,
где φ(x), ψ(x) – рациональные функции от x, . Далее,
,
где ω(x) – рациональная дробь. В последнем интеграле рациональную дробь ω(x) можно преобразовать выделением целой части и разложением на простейшие дроби. После этого получаются интегралы трех рассмотренных типов.
См. подробнее: Интегрирование рациональной функции от квадратного корня из квадратного трехчлена >>>

Интегрирование трансцендентных (тригонометрических и показательных) функций

Заранее отметим, что те методы, которые применимы для тригонометрических функций, также применимы и для гиперболических функций. По этой причине мы не будем рассматривать интегрирование гиперболических функций отдельно.

См. подробнее: Методы интегрирования тригонометрических функций >>>

Интегрирование рациональных тригонометрических функций от cos x и sin x

Рассмотрим интегралы от тригонометрических функций вида:
,
где R – рациональная функция. Сюда также могут входить тангенсы и котангенсы, которые следует преобразовать через синусы и косинусы.

При интегрировании таких функций полезно иметь в виду три правила:
1) если R( cos x, sin x ) умножается на –1 от перемены знака перед одной из величин cos x или sin x, то полезно другую из них обозначить через t.
2) если R( cos x, sin x ) не меняется от перемены знака одновременно перед cos x и sin x, то полезно положить tg x = t или ctg x = t.
3) подстановка во всех случаях приводит к интегралу от рациональной дроби. К сожалению, эта подстановка приводит к более длинным вычислениям чем предыдущие, если они применимы.

См. подробнее: Интегрирование рациональных тригонометрических функций >>>

Произведение степенных функций от cos x и sin x

Рассмотрим интегралы вида:

Если m и n – рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.

Если m и n – целые числа, то интегралы вычисляются интегрированием по частям. При этом получаются следующие формулы приведения:

;
;
;
.

См. подробнее: Интегрирование произведения степенных функций от sin x и cos x >>>

Интегрирование по частям

Интегралы, содержащие логарифм или обратные тригонометрические функции:
ln φ, arcsin φ, arctg φ, и т.д., где φ – некоторая алгебраическая функция от x, нередко интегрируются по частям, полагая u = ln φ, u = arcsin φ, u = arctg φ, и т.д.
Подробнее: Примеры решения интегралов по частям, содержащих логарифм и обратные тригонометрические функции >>>

Также по частям находятся интегралы вида:
, , ,
где P(x) – многочлен от x.
См. подробнее: Примеры решения интегралов по частям, содержащих произведение многочлена на sin x, cos x или e^x >>>

Применение формулы Эйлера

Если подынтегральное выражение линейно относительно одной из функций
cos ax или sin ax, то удобно применить формулу Эйлера:
e^iax = cos ax + isin ax (где i² = –1),
заменив эту функцию на e ^iax и выделив действительную (при замене cos ax ) или мнимую часть (при замене sin ax ) из полученного результата.

Таким способом удобно находить интегралы вида
, ,
где P(x) – многочлен от x.
См. подробнее: Интегрирование произведения многочлена, экспоненты и синуса или косинуса >>>

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов. Опубликовано: 27-09-2014

См. также: