Методы интегрирования иррациональных функций (корней)

Даны основные методы интегрирования иррациональных функций (корней). Они включают в себя: интегрирование дробно-линейной иррациональности, дифференциального бинома, интегралы с квадратным корнем из квадратного трехчлена. Приводятся тригонометрические подстановки и подстановки Эйлера. Рассмотрены некоторые эллиптические интегралы, выражающиеся через элементарные функции.

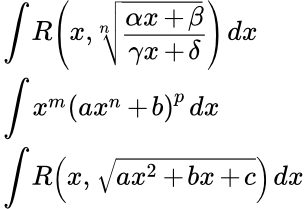
Иррациональная функция от переменной – это функция, которая образована из переменной и произвольных постоянных с помощью конечного числа операций сложения, вычитания, умножения (возведения в целочисленную степень), деления и извлечения корней. Иррациональная функция отличается от рациональной тем, что иррациональная функция содержит операции извлечения корней.

Существует три основных типа иррациональных функций, неопределенные интегралы от которых приводятся к интегралам от рациональных функций. Это интегралы, содержащие корни произвольных целочисленных степеней из дробно-линейной функции (корни могут быть различных степеней, но от одной и той же, дробно-линейной функции); интегралы от дифференциального бинома и интегралы с квадратным корнем из квадратного трехчлена.

Важное замечание. Корни многозначны!

При вычислении интегралов, содержащих корни, часто встречаются выражения вида   , где – некоторая функция от переменной интегрирования . При этом следует иметь в виду, что   . То есть, при   t > 0, |t| = t . При   t < 0, |t| = – t . Поэтому, при вычислении подобных интегралов, нужно отдельно рассматривать случаи t > 0 и t < 0. Это можно сделать, если писать знаки или там, где это необходимо. Подразумевая, что верхний знак относится к случаю t > 0, а нижний – к случаю t < 0. При дальнейшем преобразовании, эти знаки, как правило, взаимно сокращаются.

Возможен и второй подход, при котором подынтегральную функцию и результат интегрирования можно рассматривать как комплексные функции от комплексных переменных. Тогда можно не следить за знаками в подкоренных выражениях. Этот подход применим, если подынтегральная функция является аналитической, то есть дифференцируемой функцией от комплексной переменной. В этом случае и подынтегральная функция и интеграл от нее являются многозначными функциями. Поэтому после интегрирования, при подстановке численных значений, нужно выделить однозначную ветвь (риманову поверхность) подынтегральной функции, и для нее выбрать соответствующую ветвь результата интегрирования.

Далее, по возможности, мы будем применять первый подход, и следить за знаком подкоренных выражений.

Дробно-линейная иррациональность

Это интегралы с корнями от одной и той же дробно-линейной функции:
,
где R – рациональная функция,     – рациональные числа, m₁, n₁, ..., m_s, n_s – целые числа, α, β, γ, δ – действительные числа.
Такие интегралы сводится к интегралу от рациональной функции подстановкой:
, где n – общий знаменатель чисел r₁, ..., r_s.

Корни могут быть не обязательно от дробно-линейной функции, но и от линейной (γ = 0, δ = 1), или от переменной интегрирования x (α = 1, β = 0, γ = 0, δ = 1).

Вот примеры таких интегралов:
,   .

Подробнее: Интегрирование дробно-линейной иррациональности >>>

Интегралы от дифференциальных биномов

Интегралы от дифференциальных биномов имеют вид:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.

  1)   Если p – целое. Подстановка x = t ^N, где N – общий знаменатель дробей m и n.
  2)   Если – целое. Подстановка a x ⁿ + b = t ^M, где M – знаменатель числа p.
  3)   Если – целое. Подстановка a + b x ^{– n} = t ^M, где M – знаменатель числа p.

В остальных случаях, такие интегралы не выражаются через элементарные функции.

Иногда такие интегралы можно упростить с помощью формул приведения:
;
.

Подробнее: Интегрирование дифференциального бинома >>>

Интегралы, содержащие квадратный корень из квадратного трехчлена

Такие интегралы имеют вид:
,
где R – рациональная функция. Для каждого такого интеграла имеется несколько методов решения.
1)   С помощью преобразований привести к более простым интегралам.
2)   Применить тригонометрические или гиперболические подстановки.
3)   Применить подстановки Эйлера.

Рассмотрим эти методы более подробно.

1) Преобразование подынтегральной функции

Применяя формулу   ,  и выполняя алгебраические преобразования, приводим подынтегральную функцию к виду:
,
где φ(x), ω(x) – рациональные функции.
Подробнее >>>

Далее выделяя целую часть у ω(x) и раскладывая остаток на простейшие дроби, получаем интегралы трех типов.

I тип

Интеграл вида:
,
где P_n(x) – многочлен степени n.

Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:

.
Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты A_i.
Подробнее >>>

II тип

Интеграл вида:
,
где P_m(x) – многочлен степени m.

Подстановкой   t = (x – α)^–1 этот интеграл приводится к предыдущему типу. Если m ≥ n, то у дроби     следует выделить целую часть.
Подробнее >>>

III тип

.

Здесь мы делаем подстановку:
.
После чего интеграл примет вид:
.
Далее, постоянные α, β нужно выбрать такими, чтобы в знаменателе коэффициенты при t обратились в нуль:
B = 0,   B₁ = 0.
Тогда интеграл распадается на сумму интегралов двух видов:
,
,
которые интегрируются подстановками:
u ² = A₁t ² + C₁,
v ² = A₁ + C₁ t ^–2.
Подробнее >>>

2) Тригонометрические и гиперболические подстановки

В некоторых случаях, применение тригонометрических и гиперболических подстановок приводит к более коротким вычислениям. Для их применения, с помощью линейной подстановки, квадратный трехчлен под знаком интеграла нужно привести к сумме или разности квадратов. Затем нужно применить одну из тригонометрических или гиперболических подстановок. Основные подстановки перечислены ниже. Более подробно они рассматриваются на странице:
Тригонометрические и гиперболические подстановки >>>

Для интегралов вида   ,   a > 0,
имеем три основные подстановки:
;
;
;

Для интегралов   ,   a > 0,
имеем следующие подстановки:
;
;
;

И, наконец, для интегралов   ,   a > 0,
подстановки следующие:
;
;
;

Подробнее: Тригонометрические и гиперболические подстановки >>>

3) Подстановки Эйлера

Также интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
 , при a > 0;
 , при c > 0;
 , где x₁ – корень уравнения a x² + b x + c = 0. Если это уравнение имеет действительные корни.

Подробнее: Подстановки Эйлера >>>

Эллиптические интегралы

В заключении рассмотрим интегралы вида:
,
где R – рациональная функция, . Такие интегралы называются эллиптическими. В общем виде они не выражаются через элементарные функции. Однако встречаются случаи, когда между коэффициентами A, B, C, D, E существуют соотношения, при которых такие интегралы выражаются через элементарные функции.

Ниже приводится пример, связанный с возвратными многочленами. Вычисление подобных интегралов выполняется с помощью подстановок:
.

Пример

Вычислить интеграл:
.

Решение

Делаем подстановку   .

.
Здесь при x > 0 (u > 0) берем верхний знак ′+′. При x < 0 (u < 0) – нижний ′–′.

.

Ответ

.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 02-04-2015   Изменено: 30-01-2018