Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена
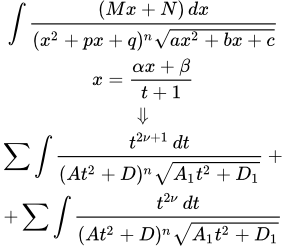
Метод интегрирования
Рассмотрим интеграл от дроби, в числителе которой стоит линейный двучлен, а в знаменателе - целая положительная степень от трехчлена и квадратный корень из квадратного трехчлена:
,
где уравнение
x 2 + px + q = 0
не имеет действительных корней. В противном случае дробь можно разложить на простейшие дроби и вычислять полученные интегралы методом, изложенном на странице Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена > > >.
Для интегрирования нужно сделать подстановку
, при b – ap ≠ 0, или подстановку
x = t + α, в противном случае.
После чего интеграл примет вид:
.
Далее, постоянные α, β нужно выбрать такими, чтобы коэффициенты при t обратились в нуль:
B = 0, B1 = 0.
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
;
.
Доказательство
Докажем, что существуют такие действительные постоянные α и β, при которых коэффициенты B и B1 обращаются в нуль.
Для доказательства, сначала упростим выражение, перейдя к новой переменной x1, сделав подстановку
x = x1 – p/2 с тем, чтобы обратить B в нуль.
.
Здесь k = q – p 2/4.
.
Отсюда видно, что если b – ap = 0, то коэффициенты при t в обоих трехчленах обращаются в нуль.
Рассмотрим случай b – ap ≠ 0. В начале заметим, что поскольку x 2 + px + q ≠ 0, то . Поэтому k > 0.
Делаем подстановку
.
Тогда уравнения равенства нулю коэффициентов при t примут вид:
Из первого уравнения, αβ = – k. Подставляя во второе уравнение, найдем α + β. Обозначим, .
Перепишем первое уравнение:
αβ = – k;
.
Отсюда . То есть r - действительное.
Таким образом, для α и β мы получили линейную систему уравнений:
α + β = 2s
α – β = 2r ,
которая имеет отличное от нуля действительное решение:
α = s + r;
β = s – r.
Примечания
Чтобы упростить доказательство и выделить случай b – ap = 0, мы сделали две подстановки:
x = x1 – p/2 и .
Однако, при вычислении интеграла, достаточно выполнить только одну дробно-линейную подстановку. Поскольку эти две, последовательно выполненные, подстановки имеют вид одной дробно-линейной :
.
При доказательстве мы предполагали, что x 2 + px + q ≠ 0. Но, поскольку оба трехчлена равноправны, то постоянные α и β существуют, и данный метод применим, если выполняется, хотя бы одно условие из двух:
x 2 + px + q ≠ 0;
ax 2 + bx + c ≠ 0.
Пример
Вычислить интеграл:
Решение
Введем обозначения:
p = x 2 – x + 1, q = x 2 + x + 1.
Делаем подстановку в общем виде, с произвольными значениями постоянных α и β: .
;
.
Выбираем α и β, чтобы коэффициенты при t обратились в нуль. Получаем систему уравнений:
Решаем систему. Берем сумму и разность уравнений:
;
;
.
Выбираем корень α = 1. Тогда β = – 1.
Делаем подстановку со значениями постоянных α = 1, β = – 1.
;
;
;
; ;
Здесь sgn(t + 1) – функция сигнум:
sgn(t + 1) = 1 при t + 1 > 0; sgn(t + 1) = – 1 при t + 1 < 0.
.
Подставляем:
.
Или
I = sgn(t + 1) · ( I1 + I2) ,
где , .
В первом интеграле делаем подстановку . ; ; ; .
.
Переходим к переменной x.
; ; ; .
Применим формулу:
.
.
.
Во втором интеграле делаем подстановку . ; ; ; .
.
Далее учтем, что . В дальнейшем верхний знак будет относиться к значениям t > 0, нижний - к значениям t < 0.
.
Умножим числитель и знаменатель на |t| = ± t и учтем, что .
.
Переходим к переменной x.
; .
Преобразуем выражение под знаком логарифма, применяя полученную ранее формулу:
.
.
Снова учтем, что .
;
.
Умножим числитель и знаменатель на . В числителе будет квадрат от . Преобразуем знаменатель.
.
Отсюда, в частности следует, что 3q > 2(x + 1) 2, поэтому и знак модуля можно опустить.
.
Окончательный результат:
I = sgn(t + 1) · ( I1 + I2) .
Ответ
Примечание
Если бы мы применили подстановку Эйлера, то получили бы интеграл:
.
Хотя подынтегральное выражение является рациональной функцией, но разложить его на простейшие дроби не так просто.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
