Подстановки Эйлера

Показано, что интегралы с рациональными функциями от квадратного корня из квадратичного многочлена сводятся к интегралам от рациональных функций с помощью подстановок Эйлера. Даны три подстановки Эйлера и рекомендации по их применению. Разобран пример вычисления интеграла с помощью подстановки Эйлера.

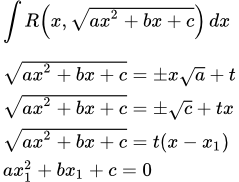
Три подстановки Эйлера

Рассмотрим интегралы, подынтегральное выражение которых является рациональной функцией от переменной интегрирования и квадратного корня из квадратного многочлена.
∫ R( x, √ ax²  + bx + c   )dx ,

Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
√ ax²  + bx + c  = ± x √ a  + t  , при a > 0 ;
√ ax²  + bx + c  = ± √ c  + tx  , при c > 0 ;
√ ax²  + bx + c  = t(x – x₁ )  , где x₁ – любой корень уравнения a x² + b x + c = 0 . Если это уравнение имеет действительные корни.

Также можно применять подстановки:
√ ax²  + bx + c  = ± x √ a  – t  , при a > 0 ;
√ ax²  + bx + c  = ± √ c  – tx  , при c > 0 ;
√ ax²  + bx + c  = – t(x – x₁ )
которые отличаются изменением знака перед t .

Выбор подстановки Эйлера

Как видно, для вычисления интеграла, можно применять не одну подстановку Эйлера. Все они приводят к интегралу от рациональной функции. Выбор в пользу той или иной подстановки следует делать, чтобы упростить вычисления.

Так, если подынтегральное выражение содержит комбинацию x – √ x²  + x + 1  , то следует выбрать подстановку Эйлера:
√ x²  + x + 1  = x + t .
Поскольку в этом случае сразу получается более простое выражение:
x – √ x²  + x + 1  = x – (x + t ) = – t

А если подынтегральное выражение содержит комбинацию 1 + √ x²  + x + 1 x , то следует выбрать подстановку:
√ x²  + x + 1  = – 1 + tx .
Поскольку в этом случае:
1 + √ x²  + x + 1 x = 1 – 1 + txx = t

Доказательство

Докажем, что подстановки Эйлера приводят к интегралу от рациональной функции.

1) a > 0

Пусть a > 0 . Делаем подстановку:
√ ax²  + bx + c  = ± x √ a  + t
Возводим в квадрат.
ax²  + bx + c = (± x √ a  + t )²  = ax²  ± 2 √ a  xt + t²
Вычитаем из обеих частей равенства ax ² и преобразовываем.
bx + c = ± 2 √ a  xt + t²
bx ∓ 2 √ a  xt = t²  – c
Отсюда видно, что x является рациональной функцией от t
x = t²  – cb ∓ 2 √ a   t
Также и дифференциал dx будет произведением рациональной функции от t на dt . И квадратный корень
√ ax²  + bx + c  = ± x √ a  + t = ± t²  – cb ∓ 2 √ a   t √ a  + t
– тоже рациональная функция от t .

То есть, при такой подстановке, подынтегральное выражение будет рациональной функцией от переменной интегрирования t .

2) c > 0

Пусть c > 0 . Делаем подстановку:
√ ax²  + bx + c  = ± √ c  + tx
Возводим в квадрат.
ax²  + bx + c = (± √ c  + tx )²  = c ± 2 √ c   tx + t² x²
Вычитаем из обеих частей равенства c и делим на x .
ax²  + bx = ± 2 √ c   tx + t² x²
ax + b = ± 2 √ c   t + t² x
ax – t² x = ± 2 √ c   t – b
Отсюда видно, что x является рациональной функцией от t
x = ± 2 √ c   t – ba – t²
Также и дифференциал dx будет произведением рациональной функции от t на dt . И квадратный корень
√ ax²  + bx + c  = ± √ c  + tx = ± √ c  + t  ± 2 √ c   t – ba – t²
– тоже рациональная функция от t .

То есть, при такой подстановке, подынтегральное выражение будет рациональной функцией от переменной интегрирования t .

3) Уравнение имеет действительные корни

Пусть уравнение a x² + b x + c = 0 имеет действительные корни x₁, x₂ . Тогда
a x² + b x + c = a(x – x₁)(x – x₂)
Делаем подстановку:
√ ax²  + bx + c  ≡ √ a(x – x₁ )(x – x₂ )  = t(x – x₁ )
Возводим в квадрат.
a(x – x₁ )(x – x₂ ) = t² (x – x₁ )²
Делим на x – x₁ и преобразовываем.
a(x – x₂ ) = t² (x – x₁ )
ax – t² x = ax₂  – t² x₁
Отсюда видно, что x является рациональной функцией от t
x = ax₂  – x₁ t²a – t²
Также и дифференциал dx будет произведением рациональной функции от t на dt . И квадратный корень
√ ax²  + bx + c  = t(x – x₁ ) = t( ax₂  – x₁ t²a – t² – x₁  )
– тоже рациональная функция от t .

То есть, при такой подстановке, подынтегральное выражение будет рациональной функцией от переменной интегрирования t .

Пример применения подстановки Эйлера

В качестве примера, вычислим интеграл
∫ dxx – √ x²  – x + 1 
применяя одну из подстановок Эйлера.

Решение

Здесь a = 1 > 0 . В соответствии со сказанным выше, для решения примера, выбираем подстановку:
√ x²  – x + 1  = x + t
Поскольку при такой подстановке, подынтегральное выражение сразу упростится
x – √ x²  – x + 1  = x – (x + t ) = – t
Возводим в квадрат и преобразовываем.
x²  – x + 1 = (x + t )²  = x²  + 2xt + t²
– x + 1 = 2xt + t²
2xt + x = 1 – t²
x = 1 – t²1 + 2t
Берем дифференциал.
dx = ( 1 – t²1 + 2t  )^′ dt = 1(1 + 2t )² ( (1 – t² )^′(1 + 2t ) –    (1 – t² )(1 + 2t )^′  ) dt =
1(1 + 2t )² ( – 2t(1 + 2t ) –    2(1 – t² ) ) dt = – 2t²  – 2t – 2(1 + 2t )²  dt = – 2  t²  + t + 1(1 + 2t )²  dt
Преобразуем знаменатель.
x – √ x²  – x + 1  = x – (x + t ) = – t

Подставляем.
I = ∫ dxx – √ x²  – x + 1  = 2 ∫ t²  + t + 1t(2t + 1 )²  dt

Разложим дробь на простейшие. Ищем разложение в виде:
2 t²  + t + 1t(2t + 1 )² = At + B(2t + 1 )² + C2t + 1
Умножаем на t(2t + 1)²
2(t²  + t + 1 ) = A(2t + 1 )²  + Bt + Ct(2t + 1 )
Подставляем t = 0,   t = –1/2,   t = – 1 .
2 = A
2( 14 – 12 + 1  ) = – 12 B
2 = A – B + C
Отсюда
А = 2
B = – 4 ⋅ 34 = – 3
C = 2 – A + B = 2 – 2 – 3 = – 3
Итак, мы получили разложение дроби на простейшие:
2 t²  + t + 1t(2t + 1 )² = 2t – 3(2t + 1 )² – 32t + 1
Интегрируем
I = 2 ln  | t |  + 32 ⋅ 12t + 1 – 32 ln  | 2t + 1 |  + C

Ответ

I = 2 ln  | t |  + 32 ⋅ 12t + 1 – 32 ln  | 2t + 1 |  + C
где
t = √ x²  – x + 1  – x

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 28-12-2014