Интегрирование простейших (элементарных) дробей
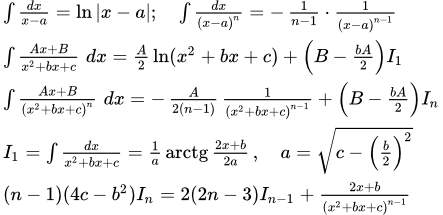
Как известно, любую рациональную функцию от некоторой переменной x можно разложить на многочлен и простейшие, элементарные, дроби. Имеется четыре типа простейших дробей:
1) 1x – a ;
2) 1(x – a ) n , n > 1 ;
3) Ax + Bx 2 + bx + c , b 2 – 4c < 0 ;
4) Ax + B(x 2 + bx + c ) n , n > 1, b 2 – 4c < 0 .
Здесь a, A, B, b, c – действительные числа. Уравнение x 2 + bx + c = 0 не имеет действительных корней.
Интегрирование дробей первых двух типов
Интегрирование первых двух дробей выполняется с помощью следующих формул из таблицы интегралов:
∫ dtt = ln | t | + C ,
∫ t n dt = 1n + 1 t n + 1 + C , n ≠ – 1 .
1. Интегрирование дроби первого типа
Дробь первого типа подстановкой t = x – a приводится к табличному интегралу:
∫ dxx – a = ∫ d(x – a )x – a = ln | x – a | + C .
2. Интегрирование дроби второго типа
Дробь второго типа приводится к табличному интегралу той же подстановкой t = x – a :
∫ dx(x – a ) n = ∫ (x – a ) – n d(x – a ) = 1– n + 1 (x – a ) – n + 1 + C =
– 1n – 1 ⋅ 1(x – a ) n – 1 + C .
3. Интегрирование дроби третьего типа
Рассмотрим интеграл от дроби третьего типа:
I = ∫ Ax + Bx 2 + bx + c dx .
Будем вычислять его в два приема.
3.1. Шаг 1. Выделим в числителе производную знаменателя
Выделим в числителе дроби производную от знаменателя. Обозначим: u = x 2 + bx + c . Дифференцируем: u′ = 2x + b . Тогда
Ax + B = A2 (2x + b ) + B – bA2 = A2 u ′ + B – bA2 ;
I = ∫ Ax + Bx 2 + bx + c dx = A2 ∫ u ′u dx + ( B – bA2 ) ∫ dxx 2 + bx + c .
Но
∫ u ′u dx = ∫dudx dxu = ∫ duu = ln | u | = ln (x 2 + bx + c ) .
Мы опустили знак модуля, поскольку x 2 + bx + c > 0 .
Тогда:
I = ∫ Ax + Bx 2 + bx + c dx = A2 ln (x 2 + bx + c ) + ( B – bA2 )I1 ,
где
I1 = ∫ dxx 2 + bx + c .
3.2. Шаг 2. Вычисляем интеграл с A = 0, B=1
Теперь вычисляем оставшийся интеграл:
I1 = ∫ dxx 2 + bx + c .
Приводим знаменатель дроби к сумме квадратов:
x 2 + bx + c = x 2 + 2x b2 + ( b2 ) 2 + c – ( b2 ) 2 = ( x + b2 ) 2 + a 2 ,
где a = √ c – ( b2 ) 2 .
Мы считаем, что уравнение x 2 + bx + c = 0 не имеет корней. Поэтому c > ( b2 ) 2 .
Сделаем подстановку
x + b2 = at, dx = a dt, t = 2x + b2a ,
x 2 + bx + c = ( x + b2 ) 2 + a 2 = a 2 (t 2 + 1 ) .
I1 = ∫ dxx 2 + bx + c = 1a ∫ dtt 2 + 1 = 1a arctg t = 1a arctg 2x + b2a .
Итак,
I1 = ∫ dxx 2 + bx + c = 1a arctg 2x + b2a , a = √ c – ( b2 ) 2 .
Тем самым мы нашли интеграл от дроби третьего типа:
I = ∫ Ax + Bx 2 + bx + c dx = A2 ln (x 2 + bx + c ) + ( B – bA2 )I1 =
A2 ln (x 2 + bx + c ) + ( B – bA2 ) 1a arctg 2x + b2a + C ,
где a = √ c – ( b2 ) 2 .
4. Интегрирование дроби четвертого типа
И наконец, рассмотрим интеграл от дроби четвертого типа:
I = ∫ Ax + B(x 2 + bx + c ) n dx .
Вычисляем его в три приема.
4.1) Выделяем в числителе производную знаменателя:
I = ∫ Ax + B(x 2 + bx + c ) n dx = – A2(n – 1 ) 1(x 2 + bx + c ) n – 1 + ( B – bA2 )In .
4.2) Вычисляем интеграл
I1 = ∫ dxx 2 + bx + c = 1a arctg 2x + b2a , a = √ c – ( b2 ) 2 .
4.3) Вычисляем интегралы
In = ∫ dx(x 2 + bx + c ) n ,
используя формулу приведения:
(n – 1 )(4c – b 2 )In = 2(2n – 3 )In – 1 + 2x + b(x 2 + bx + c ) n – 1 .
Далее мы приводим вывод этих формул, и пример вычисления интеграла от элементарной дроби четвертого типа.
4.1. Шаг 1. Выделение в числителе производной знаменателя
Выделим в числителе производную знаменателя, как мы это делали в разделе 3.1 ⇑. Обозначим u = x 2 + bx + c . Дифференцируем: u′ = 2x + b . Тогда
Ax + B = A2 (2x + b ) + B – bA2 = A2 u ′ + B – bA2 .
I = ∫ Ax + B(x 2 + bx + c ) n dx = A2 ∫ u ′u n dx + ( B – bA2 ) ∫ dx(x 2 + bx + c ) n .
Но
∫ u ′u n dx = ∫dudx dxu n = ∫ duu n = ∫ u – n du = 1– n + 1 u – n + 1 = – 1n – 1 1u n – 1 .
Окончательно имеем:
I = ∫ Ax + B(x 2 + bx + c ) n dx = – A2(n – 1 ) 1(x 2 + bx + c ) n – 1 + ( B – bA2 )In .
4.2. Шаг 2. Вычисление интеграла с n = 1
Вычисляем интеграл
I1 = ∫ dxx 2 + bx + c .
Его вычисление изложено в разделе 3.2 ⇑.
4.3. Шаг 3. Вывод формулы приведения
Теперь рассмотрим интеграл
In = ∫ dx(x 2 + bx + c ) n .
Приводим квадратный трехчлен к сумме квадратов:
x 2 + bx + c = x 2 + 2x b2 + ( b2 ) 2 + c – ( b2 ) 2 = ( x + b2 ) 2 + a 2 .
Здесь a = √ c – ( b2 ) 2 .
Делаем подстановку.
x + b2 = at, dx = a dt, t = 2x + b2a , x 2 + bx + c = a 2 (t 2 + 1 ) .
In = ∫ dx(x 2 + bx + c ) n = 1a 2n – 1 ∫ dt(t 2 + 1 ) n = 1a 2n – 1 Sn .
Выполняем преобразования и интегрируем по частям.
Sn = ∫ dt(t 2 + 1 ) n = ∫ t 2 + 1 – t 2(t 2 + 1 ) n dt = ∫ t 2 + 1(t 2 + 1 ) n dt – ∫ (t 2 + 1 ) – n t 2 dt =
∫ dt(t 2 + 1 ) n – 1 dt – 12 ∫ t (t 2 + 1 ) – n d(t 2 + 1 ) =
Sn – 1 – 12 ∫ t d( 1– n + 1 (t 2 + 1 ) – n + 1 ) =
Sn – 1 – 12 t(t 2 + 1 ) – n + 1– n + 1 + 12 ∫ (t 2 + 1 ) – n + 1– n + 1 dt =
Sn – 1 + 12(n – 1 ) t(t 2 + 1 ) n – 1 – 12(n – 1 ) Sn – 1 .
Умножим на 2(n – 1) :
2(n – 1 )Sn = 2(n – 1 )Sn – 1 – Sn – 1 + t(t 2 + 1 ) n – 1 = (2n – 3 )Sn – 1 + t(t 2 + 1 ) n – 1 .
Возвращаемся к x и In .
Sn = a 2n – 1 In , 2at = 2x + b, a 2 (t 2 + 1 ) = x 2 + bx + c, 4a 2 = 4c – b 2 ,
2(n – 1 )Sn = (2n – 3 )Sn – 1 + a 2n – 3 2at2(a 2 (t 2 + 1 )) n – 1 ;
2(n – 1 )a 2n – 1 In = (2n – 3 )a 2n – 3 In – 1 + a 2n – 3 2x + b2(x 2 + bx + c ) n – 1 ;
(n – 1 )4a 2 In = (2n – 3 )2In – 1 + 2x + b(x 2 + bx + c ) n – 1 .
Итак, для In мы получили формулу приведения:
(n – 1 )(4c – b 2 )In = 2(2n – 3 )In – 1 + 2x + b(x 2 + bx + c ) n – 1 .
Последовательно применяя эту формулу, мы сведем интеграл In к I1 .
Пример
Все примеры Вычислить интеграл
I = ∫ x + 1(x 2 + x + 1 ) 3 dx
Решение
1. Выделим в числителе производную знаменателя.
(x 2 + x + 1 ) ′ = 2x + 1 ;
x + 1 = 12 (2x + 1 ) + 12 = 12 (x 2 + x + 1 ) ′ + 12 ;
I = ∫ x + 1(x 2 + x + 1 ) 3 dx = 12 ∫ (x 2 + x + 1 ) ′(x 2 + x + 1 ) 3 dx + 12 I3 =
12 ∫ (x 2 + x + 1 ) – 3 d(x 2 + x + 1 ) + 12 I3 = 12 ⋅ 1– 3 + 1 (x 2 + x + 1 ) – 3 + 1 + 12 I3 =
– 14(x 2 + x + 1 ) 2 + 12 I3 .
Здесь
I3 = ∫ dx(x 2 + x + 1 ) 3 .
2. Вычисляем интеграл от самой простой дроби.
I1 = ∫ dxx 2 + x + 1 = ∫ dxx 2 + 2x 12 + 14 + 1 – 14 = ∫ d( x + 12 )( x + 12 ) 2 + ( √ 3 2 ) 2 =
2√ 3 arctg x + 12√ 3 2 = 2√ 3 arctg 2x + 1√ 3 .
3. Применяем формулу приведения:
(n – 1 )(4c – b 2 )In = 2(2n – 3 )In – 1 + 2x + b(x 2 + bx + c ) n – 1
для интеграла In = ∫ dx(x 2 + bx + c ) n = ∫ dx(x 2 + x + 1 ) n .
В нашем случае b = 1 , c = 1 , 4c – b 2 = 3 . Выписываем эту формулу для n = 2 и n = 3 :
3I2 = 2I1 + 2x + 1x 2 + x + 1 ;
6I3 = 6I2 + 2x + 1(x 2 + x + 1 ) 2 .
Отсюда
I3 = ∫ dx(x 2 + x + 1 ) 3 = I2 + 2x + 16(x 2 + x + 1 ) 2 =
23 I1 + 2x + 13(x 2 + x + 1 ) + 2x + 16(x 2 + x + 1 ) 2 .
Окончательно имеем:
I = – 14(x 2 + x + 1 ) 2 + 12 I3 =
– 14(x 2 + x + 1 ) 2 + 13 I1 + 2x + 16(x 2 + x + 1 ) + 2x + 112(x 2 + x + 1 ) 2 .
Находим коэффициент при 1(x 2 + x + 1 ) 2 .
– 14 + 2x + 112 = – 3 + 2x + 112 = 2x – 212 = x – 16 .
Ответ
I = 23 √ 3 arctg 2x + 1√ 3 + 2x + 16(x 2 + x + 1 ) + x – 16(x 2 + x + 1 ) 2 + C .
Автор: Олег Одинцов. Опубликовано: Изменено: