Интегрирование произведения степенных функций от sin x и cos x

Показано, что интеграл от произведения степенных функций от sin x и cos x можно привести к интегралу от дифференциального бинома. При целых значениях показателей степени, такие интегралы легко вычисляются по частям или с помощью формул приведения. Дан вывод формул приведения. Приводится пример вычисления такого интеграла.

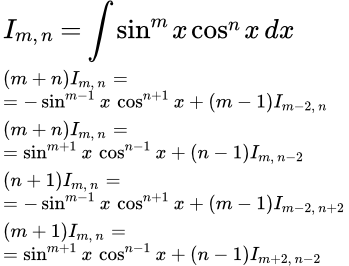
Приведение к интегралу от дифференциального бинома

Рассмотрим интегралы вида:

Такие интегралы сводятся к интегралу от дифференциального бинома одной из подстановок t = sin x или t = cos x.

Продемонстрируем это, выполнив подстановку
t = sin x.
Тогда
dt = (sin x)′ dx = cos x dx;
cos² x = 1 – sin² x = 1 – t ²;

Если m и n – рациональные числа, то следует применять методы интегрирования дифференциального бинома.
Подробнее >>>

Интегрирование с целыми m и n

Далее, рассмотрим случай, когда m и n – целые числа (не обязательно положительные). В этом случае, подынтегральное выражение является рациональной функцией от sin x и cos x. Поэтому можно применить правила, представленные в разделе «Интегрирование тригонометрических рациональных функций».
Подробнее >>>

Однако, учитывая специфические особенности, проще воспользоваться формулами приведения, которые легко получаются интегрированием по частям.

Формулы приведения

Формулы приведения для интеграла

имеют вид:

;
;
;
.

Их нет необходимости запоминать, поскольку они легко получаются интегрированием по частям.

Доказательство формул приведения

Интегрируем по частям.


Умножая на m + n, получаем первую формулу:

Аналогично получаем вторую формулу.

Интегрируем по частям.


Умножая на m + n, получаем вторую формулу:

Третья формула.

Интегрируем по частям.


Умножая на n + 1, получаем третью формулу:

Аналогично, для четвертой формулы.

Интегрируем по частям.


Умножая на m + 1, получаем четвертую формулу:

Пример

Вычислим интеграл:

Решение

Преобразуем:

Здесь m = 10, n = – 4.

Применяем формулу приведения:

При m = 10, n = – 4:

При m = 8, n = – 2:

Применяем формулу приведения:

При m = 6, n = – 0:

При m = 4, n = – 0:

При m = 2, n = – 0:

Вычисляем оставшийся интеграл:

Собираем промежуточные результаты в одну формулу.

Ответ

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 04-11-2014