Методы решения физико-математических задач

Таблица неопределенных интегралов для студентов

Таблица неопределенных интегралов
Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования.
Содержание
См. также:
()( \newcommand{\tg}{\mathop{\mathrm{tg}}\nolimits} )() ()( \newcommand{\ctg}{\mathop{\mathrm{ctg}}\nolimits} )() ()( \newcommand{\arctg}{\mathop{\mathrm{arctg}}\nolimits} )() ()( \newcommand{\arcctg}{\mathop{\mathrm{arcctg}}\nolimits} )() ()( \newcommand{\sh}{\mathop{\mathrm{sh}}\nolimits} )() ()( \newcommand{\ch}{\mathop{\mathrm{ch}}\nolimits} )() ()( \newcommand{\th}{\mathop{\mathrm{th}}\nolimits} )() ()( \newcommand{\cth}{\mathop{\mathrm{cth}}\nolimits} )() ()( \newcommand{\arsh}{\mathop{\mathrm{arsh}}\nolimits} )() ()( \newcommand{\arch}{\mathop{\mathrm{arch}}\nolimits} )() ()( \newcommand{\arth}{\mathop{\mathrm{arth}}\nolimits} )() ()( \newcommand{\arcth}{\mathop{\mathrm{arcth}}\nolimits} )()

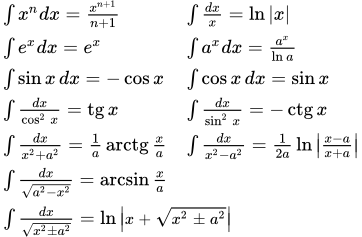
Таблица неопределенных интегралов

Ниже приводится таблица основных неопределенных интегралов. Эта таблица является основой, используемой для нахождения более сложных интегралов.

∫ x n dx = x n + 1n + 1 + C;  n ≠ – 1;  ∫ dx = x + C ;
∫ dxx = ln  | x |  + C ;
∫ e x dx = e x  + C ;   ∫ a x dx = a xln a + C  (a > 0,  a ≠ 1 ) ;
∫ sin x dx = – cos x+ C ;
∫ cos x dx = sin x+ C ;
∫ dxcos 2 x = tg x + C ;
∫ dxsin 2 x = – ctg x + C ;
∫ dx√ a 2  – x 2  = arcsin xa + C  (a > 0 ) ;   ( arcsin xa = π2 – arccos xa  )
∫ dx√ x 2  ± a 2  = ln  | x + √ x 2  ± a 2   | + C ;
∫ dxx 2  + a 2 = 1a arctg xa + C ;
∫ dxx 2  – a 2 = 12a ln  | x – ax + a  | + C .

Интегралы, связанные с гиперболическими функциями

Дополнительные формулы, имеющие отношение к гиперболическим функциям:
∫ sh x dx = ch x + C ;
∫ ch x dx = sh x + C ;
∫ dxch 2 x = th x + C ;
∫ dxsh 2 x = – cth x + C ;
∫ dx√ x 2  + a 2  = arsh xa + C;  (a > 0 ) ;
∫ dx√ x 2  – a 2  = arch xa + C;  (a > 0,  x ≥ a ) ;
∫ dx√ x 2  – a 2  = – arch ( – xa  ) + C;  (a > 0,  x ≤ – a ) ;
∫ dxx 2  – a 2 = – 1a arth xa + C;  a > 0,   | x |  < a ;
∫ dxx 2  – a 2 = – 1a arcth xa + C;  a > 0,   | x |  > a .

Таблица интегралов в дифференциальной форме

В математическом анализе большое значение имеет преобразование дифференциалов. Задачей интегрирования является сведение функции за знак дифференциала. Ниже приводится таблица интегралов в дифференциальной форме, устанавливающая связь между дифференциалами – бесконечно малыми приращениями.

x n dx = 1n + 1 dx n + 1 ;  n ≠ – 1 ;
dxx = d ln  | x |  ;
e x dx = d e x ;   a x dx = 1ln a d a x  (a > 0,  a ≠ 1 ) ;
sin x dx = – d cos x ;
cos x dx = d sin x ;
dxcos 2 x = d tg x ;
dxsin 2 x = – d ctg x ;
dx√ a 2  – x 2  = d arcsin xa  (a > 0 ) ;
dx√ x 2  ± a 2  = d ln  | x + √ x 2  ± a 2   | ;
dxx 2  + a 2 = 1a d arctg xa ;
dxx 2  – a 2 = 12a d ln  | x – ax + a  | .

Формулы, связанные с гиперболическими функциями:
sh x dx = d ch x ;
ch x dx = d sh x ;
dxch 2 x = d th x ;
dxsh 2 x = – d cth x ;
dx√ x 2  + a 2  = d arsh xa ;  (a > 0 ) ;
dx√ x 2  – a 2  = d arch xa ;  (a > 0,  x ≥ a ) ;
dx√ x 2  – a 2  = – d arch ( – xa  );  (a > 0,  x ≤ – a ) ;
dxx 2  – a 2 = – 1a d arth xa ;  a > 0,   | x |  < a ;
dxx 2  – a 2 = – 1a d arcth xa ;  a > 0,   | x |  > a .

Основные методы интегрирования

Далее f, u, v – это функции от x ; c – постоянная.
∫ d ( f (x )) =  f (x ) + C ;
∫ (u ± v ) dx = ∫ u dx ± ∫ v dx ;
∫ cu dx = c ∫ u dx ;
∫ u dv = uv – ∫ v du ;
∫  f (x ) dx = ∫  f (φ(t ))φ ′(t ) dt,  x = φ(t ) .

Автор: Олег Одинцов.     Опубликовано:   Изменено:

См. также:
▲
Меню