Вычисление производных с помощью логарифмической производной
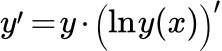
Метод решения
Пусть
(1)
есть дифференцируемая функция от переменной x. В начале мы рассмотрим ее на множестве значений x, для которых y принимает положительные значения: . В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .
В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции,
.
Отсюда
(2) .
Производная от логарифма функции называется логарифмической производной:
.
- Логарифмическая производная функции y = f(x)
- – это производная натурального логарифма этой функции: (ln f(x) )′.
Случай отрицательных значений y
Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .
Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .
Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x, отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.
Свойство логарифмической производной
Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма, формулы производной суммы и производной постоянной, имеем:
.
Примеры применений логарифмической производной
Все примерыПрименять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.
Далее мы приводим примеры вычисления производных для следующих функций:
Пример 1
Все примеры Найти производную функции:
.
Решение
Логарифмируем исходную функцию:
.
Дифференцируем по переменной x.
В таблице производных находим:
.
Применяем правило дифференцирования сложной функции.
;
;
;
;
(П1.1) .
Умножим на :
.
Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.
Примечание
Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.
Ответ
Пример 2
Все примеры С помощью логарифмической производной, найдите производную функции
.
Решение
Логарифмируем:
(П2.1) .
Дифференцируем по переменной x:
;
;
;
;
;
.
Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.
Производная исходной функции:
.
Примечание
Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.1) следует записать так:
.
Поскольку
и
,
то это не повлияет на окончательный результат.
Ответ
.
Пример 3
Все примеры Найдите производную
.
Решение
Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .
Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .
Поскольку , то
.
Примечание
Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3.1) имеем:
;
.
Сравнивая с (П3.2) мы видим, что результат не изменился.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
