Производная функции, заданной неявно
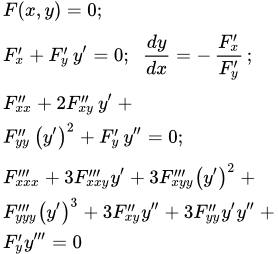
Производная первого порядка
Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .
Доказательство
Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.
Формула доказана.
Производные высших порядков
Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .
Находим производную по переменной от левой и правой части уравнения (4).
По формуле производной сложной функции имеем:
;
.
По формуле производной произведения:
.
По формуле производной суммы:
.
Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.
Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.
Продолжая дифференцирование, можно найти производную любого порядка.
Примеры
Все примеры Здесь мы рассмотрим примеры вычисления производной функций, заданных неявным образом.
Ниже рассмотрены следующие примеры.
Найти
от функции, заданной неявно уравнением:
. Найти
от функции :
. Найти
при
от функции :
.
Пример 1
Все примеры Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .
Решение по формуле 2
Находим производную по формуле (2):
(2) .
Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .
Находим производную по , считая постоянной.
;
;
;
.
Находим производную по переменной , считая переменную постоянной.
;
;
;
.
По формуле (2) находим:
.
Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.
Решение вторым способом
Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).
Применяем формулу производной сложной функции:
.
Применяем формулу производной дроби:
;
.
Применяем формулу производной сложной функции:
.
Дифференцируем исходное уравнение (П1).
(П1) ;
;
.
Умножаем на и группируем члены.
;
.
Подставим (из уравнения (П1)):
.
Умножим на :
.
Ответ
Пример 2
Все примеры Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .
Решение
Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.
Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .
Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :
;
.
Отсюда находим производную второго порядка.
Ответ
Пример 3
Все примеры Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .
Решение
Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;
Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .
Дифференцируем уравнение (П3.3).
;
;
;
;
;
(П3.4) .
Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
