Производная функции, заданной параметрическим способом
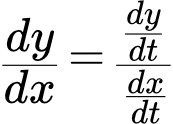
Формула производной
Пусть функция задана параметрическим способом:
(1)
где некоторая переменная, называемая параметром. И пусть функции и имеют производные при некотором значении переменной . Причем и функция имеет обратную функцию в некоторой окрестности точки . Тогда функция (1) имеет в точке производную , которая, в параметрическом виде, определяется по формулам:
(2)
Здесь и – производные функций и по переменной (параметру) . Их часто записывают в следующем виде:
;
.
Тогда систему (2) можно записать так:
Доказательство
По условию, функция имеет обратную функцию. Обозначим ее как
.
Тогда исходную функцию можно представить как сложную функцию:
.
Найдем ее производную, применяя правила дифференцирования сложной и обратной функций:
.
Правило доказано.
Доказательство вторым способом
Найдем производную вторым способом, исходя из определения производной функции в точке :
.
Введем обозначение:
.
Тогда и предыдущая формула принимает вид:
.
Воспользуемся тем, что функция имеет обратную функцию , в окрестности точки .
Введем обозначения:
; ;
; .
Разделим числитель и знаменатель дроби на :
.
При , . Тогда
.
Правило доказано.
Производные высших порядков
Чтобы найти производные высших порядков, надо выполнять дифференцирование несколько раз. Допустим, нам надо найти производную второго порядка от функции, заданной параметрическим способом, следующего вида:
(1)
По формуле (2) находим первую производную, которая также определяется параметрическим способом:
(2)
Обозначим первую производную, посредством переменной :
.
Тогда, чтобы найти вторую производную от функции по переменной , нужно найти первую производную от функции по переменной . Зависимость переменной от переменной также задана параметрическим способом:
(3)
Сравнивая (3) с формулами (1) и (2), находим:
Теперь выразим результат через функции и . Для этого подставим и применим формулу производной дроби:
.
Тогда
.
Отсюда получаем вторую производную функции по переменной :
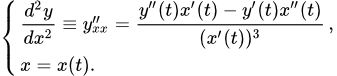
Она также задана в параметрическом виде. Заметим, что первую строку также можно записать следующим образом:
.
Продолжая процесс, можно получить производные функции от переменной третьего и более высоких порядков.
Заметим, что можно не вводить обозначение для производной . Можно записать так:
;
.
Примеры
Все примеры Здесь мы рассмотрим примеры вычисления производной функций, заданных параметрическим способом.
Ниже рассмотрены следующие примеры.
Найти
Найти
Найти производные второго и третьего порядков
Пример 1
Все примеры Найдите производную от функции, заданной параметрическим способом:
Решение
Находим производные и по .
Из таблицы производных находим:
;
.
Применяем формулу производной сложной функции:
.
Здесь .
.
Здесь .
Искомая производная:
.
Ответ
Пример 2
Все примеры Найдите производную от функции, выраженной через параметр :
Решение
Раскроим скобки, применяя формулы для степенных функций и корней:
.
Находим производную :
.
Находим производную . Для этого введем переменную и применим формулу производной сложной функции.
.
Находим искомую производную:
.
Ответ
Пример 3
Все примеры Найдите производные второго и третьего порядков от функции, заданной параметрическим способом в примере 1:
Решение
В примере 1 мы нашли производную первого порядка:
Введем обозначение . Тогда функция является производной по . Она задана параметрическим способом:
Чтобы найти вторую производную по , нам надо найти первую производную по .
Дифференцируем по .
.
Производную по мы нашли в примере 1:
.
Производная второго порядка по равна производной первого порядка по :
.
Итак, мы нашли производную второго порядка по в параметрическом виде:
Теперь находим производную третьего порядка. Введем обозначение . Тогда нам нужно найти производную первого порядка от функции , которая задана параметрическим способом:
Находим производную по . Для этого перепишем в эквивалентном виде:
.
Из таблицы производных находим:
;
.
Применяем правило дифференцирования сложной функции:
;
.
Выносим постоянную за знак производной и применяем формулу производной произведения:
.
Производная третьего порядка по равна производной первого порядка по :
.
Замечание
Можно не вводить переменные и , которые являются производными и , соответственно. Тогда можно записать так:
;
;
;
;
;
;
;
;
.
Ответ
В параметрическом представлении, производная второго порядка имеет следующий вид:
Производная третьего порядка:
Автор: Олег Одинцов. Опубликовано:
