Производная постоянной функции (константы)
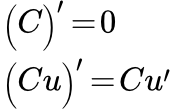
Правила дифференцирования функций, содержащих постоянные
Здесь мы рассмотрим следующие правила, связанные с дифференцированием функций, содержащих постоянные:
(1) ;
(2) ,
где C – постоянная, u – дифференцируемая функция от независимой переменной :
.
Вначале мы докажем эти правила. Затем приведем примеры вычисления производных.
Производная постоянной функции
Выясним, чему равна производная постоянной функции. Для этого применим определение производной:
(3) .
Пусть функция является постоянной, которую обозначим как :
.
То есть не зависит от x. Значения переменной y одинаковы при любых значениях переменной x и равны . Тогда
;
;
.
То есть производная постоянной функции равна нулю:
.
Вынесение постоянной за знак производной
Теперь докажем правило (2). То есть если является дифференцируемой функцией от переменной x (на некотором множестве ее значений), то при дифференцировании, постоянный множитель можно выносить за знак производной:
(2) .
Доказательство
Поскольку является дифференцируемой функцией, то существует производная этой функции:
.
Рассмотрим функцию от независимой переменной x следующего вида:
.
По определению производной
.
То есть
.
Что и требовалось доказать.
Примеры
Все примеры Проиллюстрируем применение рассмотренных правил (1) и (2). Далее будут рассмотрены примеры, в которых нужно найти производные функций, зависящих от переменной x.
⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Найти производную функции
.
Решение
Функция не содержит переменную x. Поэтому она является постоянной. Поскольку производная постоянной функции равна нулю, то производная заданной функции равна нулю:
.
Ответ
.
Пример 2
Найти производную функции от переменной x:
.
Решение
Здесь является постоянной. Выносим ее за скобки и используем таблицу производных:
.
Ответ
.
Пример 3
Найдите производную:
.
Решение
Применим свойство логарифма
.
Тогда
.
Выносим постоянную 6 за скобки и применяем таблицу производных:
.
Ответ
.
Пример 4
Продифференцировать функцию от переменной x:
.
Решение
Применим свойство экспоненты
.
Тогда
.
Но является постоянной, не зависящей от переменной величиной. Выносим ее за скобки и используем таблицу производных:
.
Ответ
.
Пример 5
Продифференцировать по переменной x функцию, состоящую из корней:
.
Решение
Преобразуем корни в степенную функцию, применяя свойства корней:
;
;
;
;
.
Выносим постоянную за скобки и применяем правило дифференцирования степенной функции из таблицы производных:
.
Тогда
.
Приведем корни к одинаковой степени и упростим результат:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
