Доказательство формулы производной сложной функции
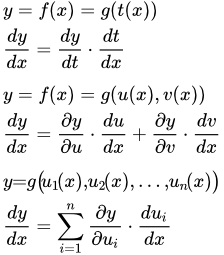
Основные формулы
Здесь мы приводим вывод следующих формул для производной сложной функции.
Пусть функцию можно представить как композицию двух функций и : . Тогда
.
Если , то
.
Если , то
.
В другой системе обозначений приведенные выше формулы можно записать так.
,
,
.
Теорема. Производная сложной функции от одной переменной
Пусть функция имеет производную при некотором значении переменной , а функция имеет производную при значении переменной .Тогда сложная (составная) функция имеет производную в точке , которая определяется по формуле:
(1.1) .
Формулу (1.1) также можно записать так:
;
.
Доказательство
Выберем значение , удовлетворяющее условию теоремы. Далее считаем, что фиксировано. То есть все последующие выкладки будем выполнять при одном и том же значении . Тогда тоже будет фиксировано.
Покажем, что существует такая окрестность точки , в которой определена сложная функция .
Поскольку существует производная , то функция определена в некоторой окрестности точки , то есть при
,
где .
Поскольку существует производная , то функция определена в некоторой окрестности точки . Также она дифференцируема в и, согласно свойству дифференцируемых функций, непрерывна в :
(1.2) ,
где .
Согласно определению предела, из (1.2) следует, что существует такая окрестность точки , принадлежащая области определения , в которой
(1.3) при ,
где .
А поскольку при функция определена, то сложная функция определена в окрестности точки , то есть при .
Теперь покажем, что .
Поскольку существуют производные и , то функции и дифференцируемы в точках и , соответственно. По определению дифференцируемой функции,
(1.4) ,
(1.5) ,
где и – бесконечно малые функции:
(1.6) ;
(1.7) .
Подставим (1.5) в (1.4).
(1.8) .
Находим производную . Для этого сначала преобразуем отношение .
.
Используем (1.8).
.
Теперь находим предел при .
;
(1.9) .
Здесь мы применили (1.7) и свойства пределов суммы и произведения учитывая, что .
В силу непрерывности функции в точке , при . Делая замену переменной в оставшемся пределе и применяя (1.6), находим.
.
С учетом этого, из (1.9) находим:
.
Формула (1.1) доказана.
Следствие
Если функцию от переменной x можно представить как сложную функцию от сложной функции
,
то ее производная определяется по формуле:
(С.1) .
Здесь , и есть некоторые дифференцируемые функции в точках , соответственно.
Эту формулу можно записать так:
.
Чтобы доказать (С.1), мы последовательно вычисляем производную по правилу дифференцирования сложной функции.
Рассмотрим сложную функцию
.
Ее производная
.
Рассмотрим исходную функцию
.
Ее производная
.
Производная сложной функции от двух переменных
Теперь пусть сложная функция зависит от нескольких переменных. Вначале рассмотрим случай сложной функции от двух переменных.
Тогда сложная функция имеет производную в точке , которая определяется по формуле:
(2.1) .
Формулу (2.1) можно записать так:
.
Доказательство
Покажем, что существует такая окрестность точки , в которой определена сложная функция .
Поскольку функция дифференцируема в точке , то она определена в некоторой окрестности этой точки. Обрежем эту окрестность так, чтобы она имела форму квадрата со стороной . То есть считаем, что определена в окрестности точки , которая дается неравенствами
(2.2) ;
(2.3) .
Поскольку существует производная , то функция определена в некоторой окрестности точки . Также она дифференцируема в и, согласно свойству дифференцируемых функций, непрерывна в :
(2.4) ,
где .
Согласно определению предела, из (2.4) следует, что существует такая окрестность точки , принадлежащая области определения , в которой
(2.5) при .
Рассуждая совершенно аналогичным способом для функции приходим к выводу, что существует такая окрестность точки , принадлежащая области определения , в которой
(2.6) при .
Возьмем . На основании (2.5) и (2.6) имеем:
и при .
То есть выполняются неравенства (2.2) и (2.3). Это означает, что при определена сложная функция .
Теперь покажем, что .
Поскольку существуют производные и , то функции и дифференцируемы в точке . По определению дифференцируемой функции
(2.7) ,
(2.8) ,
где и – бесконечно малые функции:
(2.9) ;
(2.10) .
По условию теоремы дифференцируема в точке . Тогда ее приращение в этой точке можно представить в следующем виде.
(2.11) , где
(2.12) .
Здесь мы для краткости отбросили аргументы производных: .
Подставим (2.7), (2.8) в (2.11).
(2.13)
.
Здесь также .
Находим производную . Для этого сначала преобразуем отношение .
.
Используем (2.13).
.
Теперь находим предел при .
;
(2.14) .
Здесь мы применили (2.9), (2.10) и свойства пределов суммы и произведения учитывая, что .
В силу непрерывности функций и в точке , и при . Делая замену переменной в оставшемся пределе и применяя (2.12), находим.
.
С учетом этого, из (2.14) находим:
.
Формула (2.1) доказана.
Производная сложной функции от нескольких переменных
Приведенный выше вывод легко обобщается на случай, когда число переменных сложной функции больше двух.
Например, если g является функцией от трех переменных, то
,
где
, и есть дифференцируемые функции при некотором значении переменной x;
– дифференцируемая функция, от трех переменных, в точке , , .
Тогда, из дифференцируемости функции , имеем:
(3.1)
,
где
.
В силу непрерывности ,
; ; .
Тогда
;
;
.
Разделив (3.1) на и выполнив предельный переход , получим:
.
Или
.
И, наконец, рассмотрим самый общий случай.
Пусть функцию от переменной x можно представить как сложную функцию от n переменных в следующем виде:
,
где
есть дифференцируемые функции при некотором значении переменной x;
– дифференцируемая функция от n переменных в точке
.
Тогда
.
Или
.
Автор: Олег Одинцов. Опубликовано: Изменено:
