Теорема об изменении кинетической энергии. Пример решения задачи.
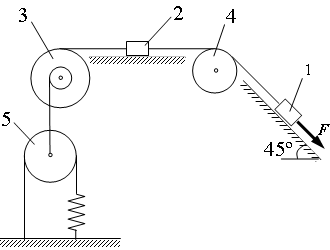
Условие задачи

Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и подвижного блока 5. Блок 5 считать сплошным однородным цилиндром. Коэффициент трения груза 2 о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с = 280 Н/м.
Под действием силы F = f(s) = 80(6 + 7s) Н, зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M = 1,6 Н·м сил сопротивления (от трения в подшипниках). Массы тел: m1 = 0, m2 = 5 кг, m3 = 6 кг , m4 = 0, m5 = 4 кг.
Определить значение центра масс тела 5 VC5 в тот момент времени, когда перемещение s груза 1 станет равным s1 = 0,2 м.
Указание. При решении задачи использовать теорему об изменении кинетической энергии.
Решение задачи
Дано: R3 = 0,3 м, r3 = 0,1 м, ρ3 = 0,2 м, R4 = 0,2 м, f = 0,1, с = 280 Н/м, m1 = 0, m2 = 5 кг, m3 = 6 кг , m4 = 0, m5 = 4 кг, F = f(s) = 80(6 + 7s) Н, s1 = 0,2 м.
Найти: VC5.
Обозначения переменных
R3 , r3 – радиусы ступеней шкива 3;
ρ3 – радиус инерции шкива 3 относительно оси вращения;
R5 – радиус блока 5;
V1, V2 – скорости тел 1 и 2;
ω3 – угловая скорость вращения шкива 3;
VC5 – скорость центра масс C5 блока 5;
ω5 – угловая скорость вращения блока 5;
s1, s2 – перемещение тел 1 и 2;
φ3 – угол поворота шкива 3;
sC5 – перемещение центра масс C5 блока 5;
sA, sB – перемещение точек A и B.
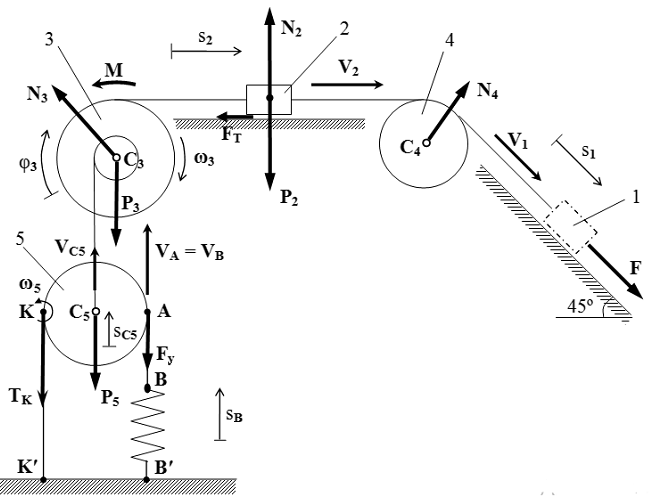
Установление кинематических соотношений
Установим кинематические соотношения. Поскольку грузы 1 и 2 связаны одной нитью, то их скорости равны:
V2 = V1.
Поскольку нить, соединяющая грузы 1 и 2 намотана на внешнюю ступень шкива 3, то точки внешней ступени шкива 3 движутся со скоростью V2 = V1. Тогда угловая скорость вращения шкива:
.
Скорость центра масс VC5 блока 5 равна скорости точек внутренней ступени шкива 3:
.
Скорость точки K равна нулю. Поэтому она является мгновенным центром скоростей блока 5. Угловая скорость вращения блока 5:
.
Скорость точки B – свободного конца пружины – равна скорости точки A:
.
Выразим скорости через VC5.
;
;
.
Теперь установим связи между перемещениями тел и углами поворота шкива и блока. Поскольку скорости и угловые скорости являются производными по времени от перемещений и углов поворота
,
то такие же связи будут между перемещениями и углами поворота:
s2 = s1;
;
;
.
Определение кинетической энергии системы
Найдем кинетическую энергию системы. Груз 2 совершает поступательное движение со скоростью V2. Шкив 3 совершает вращательное движение с угловой скоростью вращения ω3. Блок 5 совершает плоскопараллельное движение. Он вращается с угловой скоростью ω5 и его центр масс движется со скоростью VC5. Кинетическая энергия системы:
.
Поскольку радиус инерции шкива относительно оси вращения задан, то момент инерции шкива относительно оси вращения определяется по формуле:
J3 = m3 ρ23.
Поскольку блок 5 является сплошным однородным цилиндром, то его момент инерции относительно центра масс равен
.
С помощью кинематических соотношений выражаем все скорости через VC5 и подставляем выражения для моментов инерции в формулу для кинетической энергии.
,
где мы ввели постоянную
кг.
Итак, мы нашли зависимость кинетической энергии системы от скорости центра масс VC5 подвижного блока:
, где m = 75кг.
Определение суммы работ внешних сил
Рассмотрим внешние силы, действующие на систему.
При этом мы не рассматриваем силы натяжения нитей, поскольку нити нерастяжимые и, поэтому, они не производят работу. По этой причине мы не рассматриваем внутренние напряжения, действующие в телах, поскольку они являются абсолютно твердыми.
На тело 1 (с нулевой массой) действует заданная сила F.
На груз 2 действует сила тяжести P2 = m2 g, сила давления поверхности N2 и сила трения FT.
На шкив 3 действует сила тяжести P3 = m3 g, сила давления оси N3 и момент сил трения M.
На шкив 4 (с нулевой массой) действует сила давления оси N4.
На подвижный блок 5 действует сила тяжести P5 = m5 g, сила упругости Fy пружины и сила натяжения нити TK в точке K.
Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними. Заданная сила , приложенная к телу 1, параллельна перемещению тела 1. Поэтому работа, которую совершает сила , при перемещении тела 1 на расстояние s1 равна:
Дж.
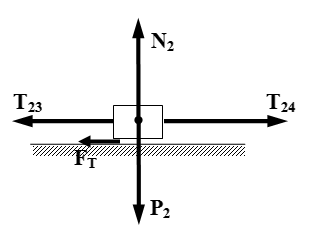
Рассмотрим груз 2. На него действуют сила тяжести P2, сила давления поверхности N2, силы натяжения нитей T23, T24 и сила трения FT. Поскольку груз не совершает перемещения в вертикальном направлении, то проекция его ускорения на вертикальную ось равна нулю. Поэтому сумма проекций сил на вертикальную ось равна нулю:
N2 – P2 = 0;
N2 = P2 = m2 g.
Сила трения:
FT = f N2 = f m2 g.
Силы P2 и N2 перпендикулярны перемещению s2, поэтому они работу не производят.
Работа силы трения:
Дж.
Если рассматривать груз 2 как изолированную систему, то нужно учитывать работу, произведенную силами натяжения нитей T23 и T24. Однако нас интересует вся система, состоящая из тел 1, 2, 3, 4 и 5. Для такой системы силы натяжения нитей являются внутренними силами. А поскольку нити нерастяжимые, то сумма их работ равна нулю. В случае с грузом 2, нужно еще учесть силы натяжения нитей, действующих на шкив 3 и блок 4. Они равны по величине и противоположны по направлению силам T23 и T24. Поэтому работа, производимая силами натяжения нитей 23 и 24 над грузом 2 равна по величине и противоположна по знаку работе, производимой силами натяжения этих нитей над шкивом 3 и блоком 4. В результате сумма работ, производимая силами натяжения нитей равна нулю.
Рассмотрим шкив 3. Поскольку его центр масс не перемещается, то работа силы тяжести P3 равна нулю.
Поскольку ось C3 неподвижна, то сила давления оси N3 работу не производит.
Работа, произведенная моментом сил , вычисляется аналогично работе, произведенной силой :
.
В нашем случае, векторы момента сил трения и угла поворота шкива направлены вдоль оси вращения шкива, но противоположны по направлению. Поэтому работа момента сил трения:
Дж.
Рассмотрим блок 5.
Поскольку скорость точки K равна нулю, то сила TK работу не производит.
Центр масс блока C5 переместился на расстояние sC5 вверх. Поэтому работа силы тяжести блока равна:
Дж.
Работа силы упругости пружины равна изменению потенциальной энергии пружины со знаком минус. Поскольку вначале пружина не деформирована, то
Дж.
Сумма работ всех сил:
Дж.
Применение теоремы об изменении кинетической энергии системы
Применим теорему об изменении кинетической энергии системы в интегральной форме.
.
Поскольку в начале система покоилась, то ее кинетическая энергия в начале движения
T0 = 0.
Тогда
.
Отсюда
м/с.
Ответ
м/с.
Автор: Олег Одинцов. Опубликовано:
