Основные формулы прямолинейного движения
Пусть материальная точка движется по оси . Далее и обозначают координату и скорость точки в начальный момент времени .
Если задан закон изменения ее координаты от времени:
,
то дифференцируя координату по времени, получаем скорость и ускорение точки:
;
.
Пусть нам известна зависимость ускорения от времени:
.
Тогда зависимости скорости и координаты от времени определяются по формулам:
(1) ;
(2) ;
(3) ;
(4) .
Пусть нам известна зависимость ускорения от координаты:
.
Тогда зависимость скорости от координаты имеет вид:
(5) .
Зависимость координаты от времени определяется в неявном виде:
(6) .
Для прямолинейного равномерного движения:
;
;
.
Для прямолинейного равноускоренного движения:
;
;
;
.
Приведенные здесь формулы можно применить не только для прямолинейного движения, но и для некоторых случаев криволинейного движения. Например для трехмерного движения в прямоугольной системе координат , если движение вдоль оси не зависит от проекций величин на другие координатные оси. Тогда формулы (1) – (6) дают зависимости для проекций величин на ось .
Также эти формулы применимы при движении по заданной траектории при естественном способе задания движения. Только здесь в качестве координаты выступает длина дуги траектории, отсчитываемая от выбранного начала отсчета . Тогда вместо проекций и следует подставить и – проекции скорости и ускорения на выбранное направление касательной к траектории.
Прямолинейное движение при известной зависимости координаты от времени
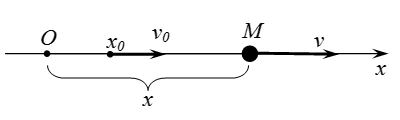
Рассмотрим случай, когда материальная точка движется по прямой линии. Выберем систему координат с началом в произвольной точке . Ось направим вдоль линии движения точки. Тогда положение точки однозначно определяется значением одной координаты .
Если задан закон изменения координаты от времени :
,
то дифференцируя по времени , найдем закон изменения скорости:
.
При точка движется в положительном направлении оси (на рисунке слева направо). При точка движется в отрицательном направлении оси (на рисунке справа налево).
Дифференцируя скорость по времени, находим закон изменения ускорения:
.
Поскольку прямая не имеет кривизны, то радиус кривизны траектории можно считать бесконечно большим, . Тогда нормальное ускорение равно нулю:
.
То есть ускорение точки тангенциальное (касательное):
.
Что вполне естественно, поскольку и скорость и ускорение точки направлены по касательной к траектории – прямой, вдоль которой происходит движение.
Если и одного знака (то есть оба положительные или оба отрицательные), то модуль скорости увеличивается (скорость возрастает по абсолютной величине). Если и разных знаков, то модуль скорости уменьшается (скорость убывает по абсолютной величине).
Прямолинейное движение при известном ускорении
Ускорение, зависящее от времени
Пусть нам известен закон изменения ускорения от времени:
.
Нашей задачей является найти закон изменения скорости и закон изменения координаты от времени:
;
.
Применим формулу:
.
Это дифференциальное уравнение первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем:
;
.
Здесь – постоянная интегрирования. Отсюда видно, что только по известной зависимости ускорения от времени, нельзя однозначно определить зависимость скорости от времени. Мы получили целое множество законов изменения скорости, которые отличаются друг от друга на произвольную постоянную . Чтобы найти нужный нам закон изменения скорости, мы должны задать еще одно значение. Как правило таким значением является значение скорости в начальный момент времени . Чтобы это сделать перейдем от неопределенного интеграла к определенному:
.
Пусть – скорость точки в начальный момент времени . Подставим :
;
;
.
Таким образом закон изменения скорости от времени имеет вид:
(1) .
Аналогичным образом определяем закон изменения координаты от времени.
.
(2) .
Здесь – значение координаты в начальный момент времени .
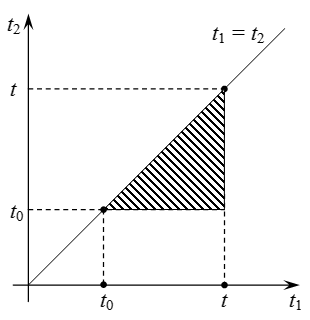
Если изменить порядок интегрирования в двойном интеграле, то получим:
.
Таким образом, мы получили следующие формулы:
(3) ;
(4) .
Ускорение, зависящее от координаты
Пусть теперь нам известен закон изменения ускорения от координаты:
.
Нам нужно решить дифференциальное уравнение:
.
Это дифференциальное уравнение не содержит независимую переменную в явном виде. Общий метод решения таких уравнений рассмотрен на странице “Дифференциальные уравнения высших порядков, не содержащие независимую переменную в явном виде”. Согласно этому методу мы считаем, что является функцией от :
;
.
Разделяем переменные и интегрируем:
;
;
;
.
Извлекая корень нужно учесть, что скорость может быть как положительной, так и отрицательной. На небольшом удалении от точки , знак определяется знаком постоянной . Однако, если ускорение направлено противоположно скорости, то скорость точки уменьшится до нуля и направление движения изменится на противоположное. Поэтому правильный знак, плюс или минус, выбирается при рассмотрении конкретного движения.
(5) .
В начале движения
.
Теперь определяем зависимость координаты от времени. Дифференциальное уравнение для координаты имеет вид:
.
Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:
(6) .
Это уравнение определяет зависимость координаты от времени в неявном виде.
Прямолинейное равномерное движение
Применим полученные выше результаты для случая прямолинейного равномерного движения. В этом случае ускорение
.
По формулам (1) и (2) находим:
;
. То есть скорость является постоянной, а координата линейно зависит от времени. Формулы (5) и (6) дают тот же самый результат.
Прямолинейное равноускоренное движение
Теперь рассмотрим прямолинейное равноускоренное движение.
В этом случае ускорение является величиной постоянной:
.
По формулам (1) и (2) находим:
;
.
Если применим формулу (5), то получим зависимость скорости от координаты:
.
Прямолинейное движение в векторном виде
Полученные формулы можно представить в векторном виде. Для этого достаточно умножить уравнения, определяющие , и на единичный вектор (орт) , направленный вдоль оси .
Тогда радиус-вектор точки, векторы скорости и ускорения имеют вид:
;
;
.