Дифференциальные уравнения первого порядка, приводящиеся к однородным
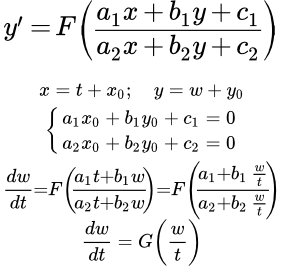
К однородным дифференциальным уравнениям первого порядка приводятся уравнения вида
,
где и – однородные функции с равными показателями однородности p. То есть функции, обладающие свойством
.
Такие уравнения можно выразить через одну функцию F:
.
См. Общий вид ДУ, приводящихся к однородным.
Если система
имеет единственное решение , то такие уравнения приводятся к однородным подстановками .
Как определить, что дифференциальное уравнение приводится к однородному
Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:
,
и выполнить замены:
.
Если, после преобразований, t сократится, и уравнение будет содержать только и , то это уравнение приводится к однородному.
Пример
Определить, приводится ли данное дифференциальное уравнение к однородному:
.
Решение
Выделяем две линейные формы:
.
В исходном уравнении делаем замены: .
;
.
По свойству логарифма:
.
t сокращается, и уравнение не содержит в явном виде переменные x и y:
.
Следовательно, это уравнение приводится к однородному.
Метод решения, приводящегося к однородному, дифференциального уравнения
Рассмотрим дифференциальное уравнение вида(М.1) ,
где и – однородные функции с равными показателями однородности p:
(М.2) .
Тогда оно приводится либо к однородному уравнению, либо к уравнению с разделяющимися переменными.
Две формы уравнения
Покажем, что уравнение (М.1) можно записать в более удобной форме
(М.3) .
Введем обозначения
.
Разделим (М.1) на , и применим (М.2).
При имеем:
; ; ; ;
.
Здесь – функция, зависящая только от отношения .
Далее следует рассмотреть случай
(М.4) ,
который мы исключили из рассмотрения при переходе от (М.1) к (М.3). В (М.1) могут дополнительно присутствовать решения, определяемые из (М.4), которых нет в (М.3). В остальном множества решений этих уравнений совпадают. При доказательстве мы будем использовать более простую форму (М.3).
Решения системы уравнений
Методом Крамера решаем систему уравнений:
(М.5)
;
;
.
Здесь возможны три случая.
1. Система имеет единственное решение, (прямые и пересекаются в одной точке).
2. Система имеет бесконечное множество решений, (прямые совпадают).
3. Система не имеет решений, (прямые параллельны).
1. Система имеет одно решение
Пусть система (М.5) имеет одно решение :
(М.6)
Сделаем в (М.3) подстановку x = t + x0, y = w + y0, и применим (М.6). Здесь w – функция от t. Тогда
dx = dt, dy = dw;
.
Или
.
Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой , где – функция от .
2. Система имеет бесконечное множество решений
Пусть система (М.5) имеет бесконечное множество решений. В этом случае имеется только одно линейно независимое уравнение. Первое получаются из второго, умножением на постоянную:
;
.
Тогда
;
.
Это простейший вид уравнения с разделяющимися переменными:
.
Его решение:
.
Здесь .
3. Система не имеет решений
Пусть система (М.5) не имеет решений. В этом случае
.
Тогда
;
.
Здесь .
Также мы ввели обозначения .
Подставляем в уравнение (М.3).
;
.
То есть в этом случае правая часть уравнения является функцией от . Ранее мы нашли, что такое уравнение приводится к уравнению с разделяющимися переменными подстановкой
.
Пример решения, приводящегося к однородному, дифференциального уравнения первого порядка
Решить уравнение
(П.1) .
Решение
1) Проверим, приводится ли это дифференциальное уравнение к однородному. Для этого выделяем две линейные формы:
и .
Первую заменим на , вторую – на :
.
Делим на t:
.
t сократилось, и уравнение содержит в явном виде только и производную . Поэтому оно приводится к однородному.
2) Решаем систему
Из первого уравнения y = 2x + 4. Подставляем во второе:
x – 2(2x + 4) + 5 = 0;
x – 4x – 8 + 5 = 0;
– 3x = 3;
x = –1;
y = 2x + 4 = 2·(–1) + 4 = 2.
Итак, мы нашли решение системы:
x0 = –1, y0 = 2.
3) Делаем подстановки:
;
,
где w – функция от t.
dx = dt, dy = dw, ;
;
.
Подставляем в (П.1):
(П.2) .
4) Решаем однородное уравнение (П.2). Делаем подстановку:
, где – функция от t.
.
Подставляем в (П.2):
.
Сокращаем на t и выполняем преобразования:
;
;
.
Разделяем переменные – умножаем на , и делим на .
При получаем:
.
Интегрируем:
(П.3) .
Вычисляем интегралы:
;
.
Подставляем в (П.3):
.
Умножим на 2 и потенцируем:
;
.
Заменим постоянную . Раскроем знак модуля, после чего постоянная сможет принимать отрицательные значения. Умножим на и применим формулу: .
.
Сократим на :
.
Возвращаемся к переменным w и t, используя формулу: . Для этого умножим на t:
;
;
.
Возвращаемся к переменным x и y, используя формулы: t = x + 1, w = y – 2.
;
(П.4) .
Теперь рассмотрим случай или .
;
.
Для верхнего знака «+» имеем:
;
.
Это решение входит в общий интеграл (П.4) при значении постоянной C = 0.
Для нижнего знака «–»:
;
.
Эта зависимость также является решением исходного дифференциального уравнения, но не входит в общий интеграл (П.4). Поэтому к общему интегралу добавим решение
.
Ответ
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
