Формула Коши для повторных интегралов

Доказана формула Коши, которая сводит повторные интегралы от некоторой функции f к однократному. Показано, что эти интегралы являются частным решением дифференциального уравнения, в котором производная n-ой степени от y равна f(x), с нулевыми начальными условиями. Дано общее решение такого уравнения.

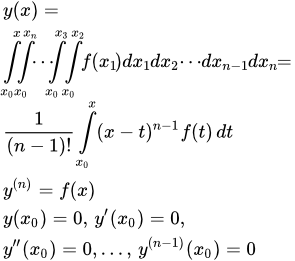
Формула Коши

Формула Коши позволяет свести повторный n-кратный интеграл к однократному:
(1)  
.
Здесь f – интегрируемая на отрезке функция. При этом является частным решением дифференциального уравнения
(2)  
с начальными условиями
(3)   .

Часто в литературе повторный интеграл записывают так:
.

Решение дифференциального уравнения y⁽ⁿ⁾=f(x)

Рассмотрим дифференциальное уравнение
.
Изменим обозначение переменной x на :
.
Проинтегрируем по от до x:

;
.

Часто, во входящем сюда интеграле, для переменной интегрирования используют такое же обозначение, как и для верхнего предела интегрирования: . Это делают только с одной целью – уменьшить количество используемых переменных и получить более короткие формулы. Однако такая форма записи может привести к заблуждению. Для обозначения переменной интегрирования и пределов интегрирования лучше использовать различные переменные.

Переименуем переменную x на , и проинтегрируем по от до x:
;
;
;
.
Тем же способом интегрируем еще раз:
;

;

;

.

Выполняя интегрирование n раз, получим решение исходного дифференциального уравнения с начальными условиями   :
(4)  
.

Отсюда видно, что если положить , то повторный интеграл

является частным решением дифференциального уравнения (2) с начальными условиями
.

Формула (4) дает нам общее решение дифференциального уравнения (2). В правой части она содержит многочлен степени n. Если перейти к новым постоянным, то общее решение можно записать так:
.

Сведение повторного интеграла к однократному

Таким образом, для решения задачи, нам нужно проинтегрировать функцию n раз. Но оказывается, что стоящий в (4) интеграл можно преобразовать так, что задача сведется к вычислению только одного интеграла.

Случай n = 2

Для начала, возьмем случай . Рассмотрим входящий в (4) двукратный интеграл
(5)   .
Изменим порядок интегрирования.

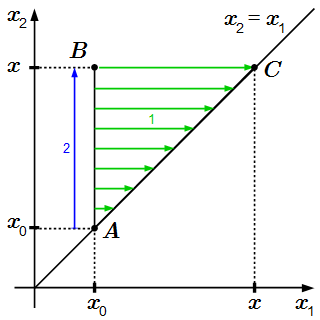
Изобразим область интегрирования на рисунке. Проводим оси координат . Проведем прямую . В (5) мы сначала интегрируем по переменной от до прямой . Затем мы интегрируем по переменной от до x. Областью интегрирования является множество точек треугольника ABC с вершинами .

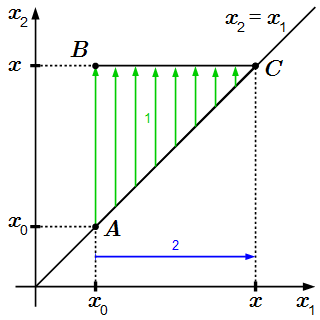
Изменим порядок интегрирования. Сначала проинтегрируем по переменной от прямой до x, а затем по от до x. Тогда
(6)   .
Поскольку функция f не зависит от переменной , то в первом интеграле она является постоянной. Это позволяет нам его вычислить:
.
Подставим в (6):
.
Видно, что при изменении порядка интегрирования, мы смогли вычислить один интеграл. В результате повторное интегрирование свелось к однократному интегралу:
(7)   .

Случай n = 3

Далее можно рассмотреть случай :
(8)   .
Используем формулу (7), в которой заменим x на :
.
Применим ее для трехкратного интеграла (8):
.
Теперь поменяем порядок интегрирования, как мы это делали ранее ⇑, только вместо переменной у нас будет :
(9)   .
Вычисляем первый интеграл:

;
Подставляем в (9):
.

Это наводит нас на мысль, что в общем случае, для произвольного n, повторный интеграл сводится к однократному по следующей формуле:
.
Докажем это методом математической индукции.

Доказательство формулы Коши

Автор: Олег Одинцов.     Опубликовано: 18-11-2020