Непрерывность функций – содержание раздела
Содержание раздела "Непрерывность функций" в картинках. Приводятся заголовки, главные изображения и описание содержания страниц. Каждая картинка в сжатом виде отображает главную мысль страницы, на которую ведет ссылка.
Непрерывность функций – теоремы и свойства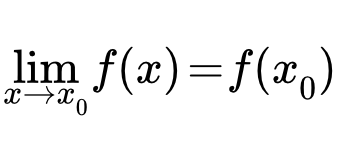
Приводятся определения и формулировки основных теорем и свойств непрерывной функции одной переменной. Рассмотрены свойства непрерывной функции в точке, на отрезке, предел и непрерывность сложной функции, классификация точек разрыва. Даны определения и теоремы, связанные с обратной функцией. Изложены свойства элементарных функций. Определение непрерывности функции в точке
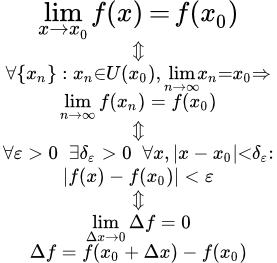Приводится определение непрерывности функции в точке. Рассмотрены эквивалентные определения по Гейне, по Коши и в терминах приращений. Определение односторонней непрерывности на концах отрезка. Формулировка отсутствия непрерывности. Разобраны примеры, в которых требуется доказать непрерывность функции, используя определения по Гейне и по Коши. Свойства непрерывных в точке функций
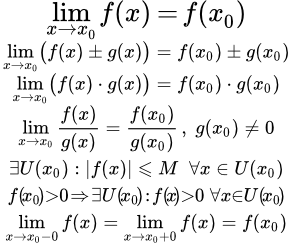Приводятся доказательства основных свойств и теорем, непрерывных в точке функций. Сюда входят: арифметические свойства, теорема об ограниченности, теорема о сохранении знака, свойство односторонней непрерывности. Предел и непрерывность сложной функции
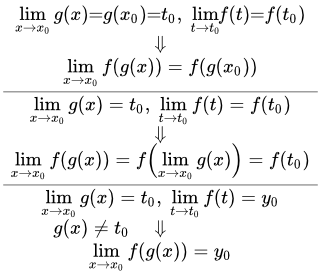Рассмотрены следующие теоремы: теорема о непрерывности сложной функции; теорема о пределе непрерывной функции от функции; теорема о пределе сложной функции. Доказательства этих теорем. Точки разрыва функции – определения, классификация и примеры
Определения точек разрыва первого и второго рода. Основные факты, используемые при исследовании функций на непрерывность. Примеры решения задач, в которых требуется найти точки разрыва и определить вид разрыва. 
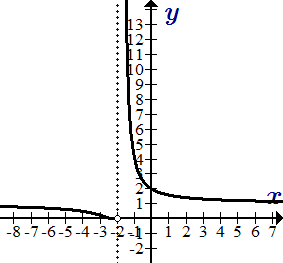График функции y = 41/(x+2). 
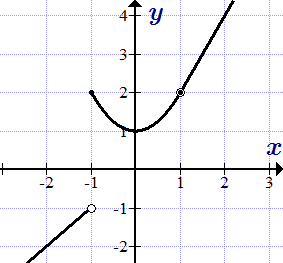График заданной функции. Свойства функций, непрерывных на отрезке
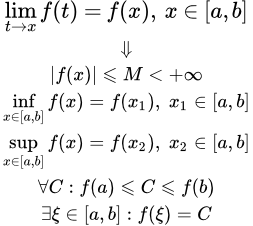Определение и формулировки основных теорем для функций, непрерывных на отрезке. Сюда входят: первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции; вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции; теорема Больцано – Коши о промежуточном значении. Теоремы Вейерштрасса о непрерывных на отрезке функциях
Доказательства первой и второй теорем Вейерштрасса об ограниченности и достижении максимума и минимума непрерывной на отрезке функции. Теорема Больцано – Коши о промежуточном значении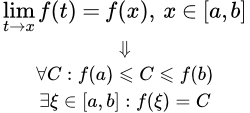
Формулировка и доказательство теоремы Больцано – Коши о промежуточном значении функции, непрерывной на отрезке . Обратные функции – определение и свойства
Определение обратной функции и ее свойства: теорема о взаимной монотонности прямой и обратной функций; симметрия графиков прямой и обратной функций; теоремы о существовании и непрерывности обратной функции для функции, строго монотонной на отрезке, интервале и полуинтервале. Примеры обратных функций. Пример решения задачи.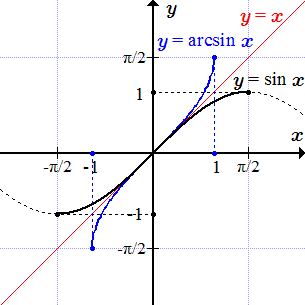 
Графики y = sin x и обратной функции y = arcsin x. 
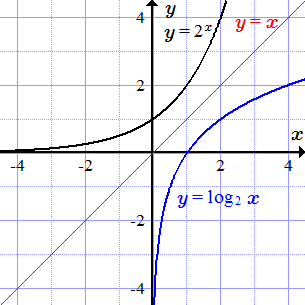Графики y = 2x и обратной функции y = log2 x. 
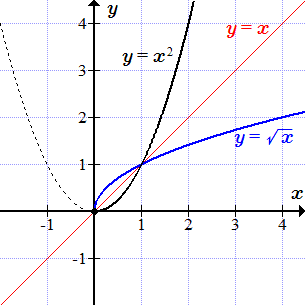Графики y = x2 и обратной функции y = √x. Теорема о существовании и монотонности обратной функции
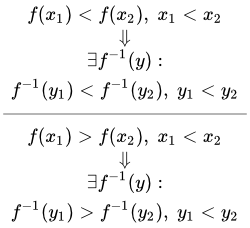Формулировка и доказательство теоремы о существовании и монотонности обратной функции. График обратной функции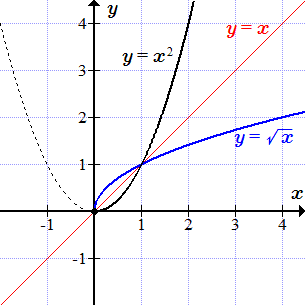Доказательство свойства симметрии графиков прямой и обратной функций. Примеры графиков прямых и обратных функций: параболы и корни, степенные функция и логарифмы, тригонометрические функции и обратные к ним. Применение операции сужения функции. 
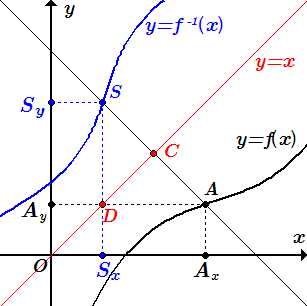График обратной функции y = f –1(x) симметричен графику прямой функции y = f(x) относительно прямой y = x. 
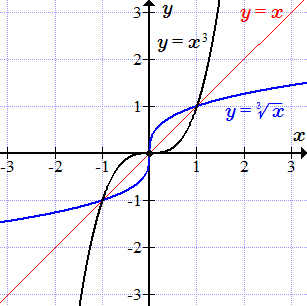График кубической параболы y = x3 и обратной функции – кубического корня y = √3x. График показательной функции с основанием 2, y = 2x и обратной функции – логарифма с основанием 2, y = log2 x.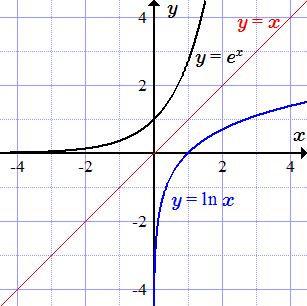 
График экспоненты y = ex и обратной функции – натурального логарифма y = ln x. График синуса y = sin x и обратной функции – арксинуса y = arcsin x.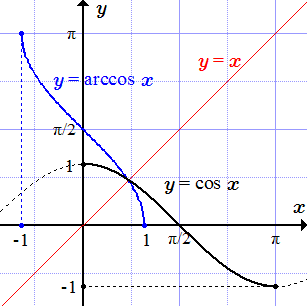 
График косинуса y = cos x и обратной функции – арккосинуса y = arccos x. 
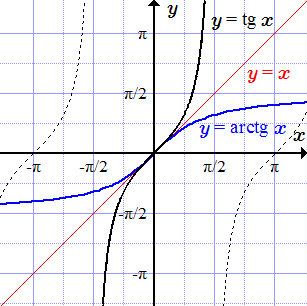График тангенса y = tg x и обратной функции – арктангенса y = arctg x. 
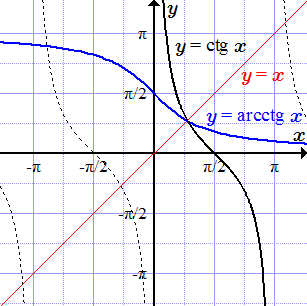График котангенса y = ctg x и обратной функции – арккотангенса y = arcctg x. Теоремы о существовании и непрерывности обратной функции
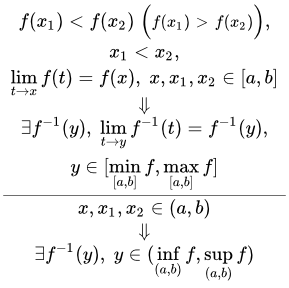Доказательство теорем о существовании и непрерывности обратной функции. Рассмотрены три теоремы для строго монотонной функции на отрезке, интервале и полуинтервале. 
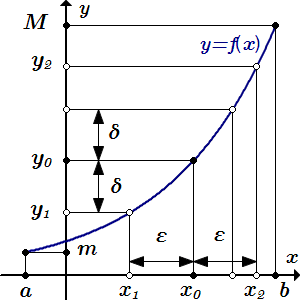Для любого ε > 0 существует δ, так что |f -1(y) – f -1(y0)| < ε для всех |y – y0| < δ. 
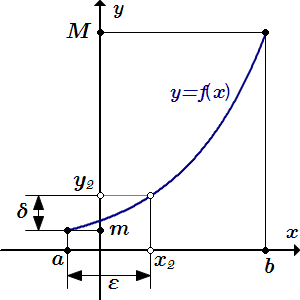Для любого ε > 0 существует δ, так что f -1(y) – f -1(m) < ε для всех y – a < δ. 
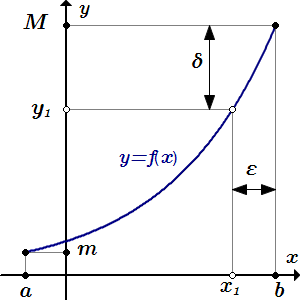Для любого ε > 0 существует δ, так что f -1(M) – f -1(y) < ε для всех M – y < δ. Неравенства и лемма Бернулли
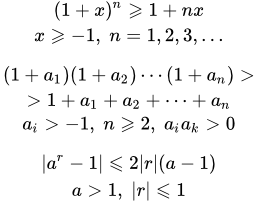Дано неравенство Бернулли и его следствие, которое называется леммой Бернулли. Неравенство приводится в двух формах. Приводятся доказательства неравенств и леммы. Определение и свойства показательной функции
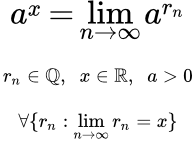Определение и свойства показательной функции на множестве натуральных, целых и рациональных чисел. Определение на множестве действительных чисел посредством предела последовательности. Теорема о свойствах показательной функции. Свойства показательной функции
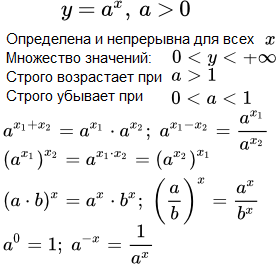Доказательство теоремы о свойствах показательной функции на множестве действительных чисел. Свойства включают: область определения, множество значений, непрерывность, формулы с показательной функцией. Определение и доказательство свойств логарифма
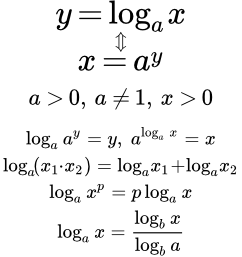Дано определение логарифма с основанием a как функции, обратной к показательной. Основываясь на свойствах показательной функции и теореме об обратной функции, дается вывод свойств логарифма. Непрерывность и свойства степенной функции
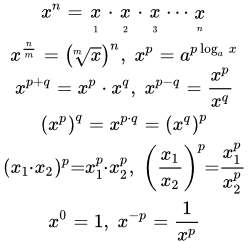Дано определение степенной функции. Показано, что ее можно представить как сложную, составленную из логарифмической и показательной функций. Основываясь на их свойствах, дается доказательство непрерывности и вывод свойств степенной функции. 
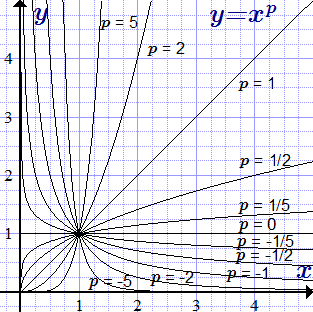Графики степенной функции y = x p при различных значениях показателя p. Доказательство непрерывности тригонометрических функций
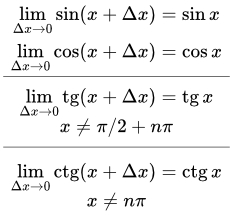Дано доказательство непрерывности тригонометрических функций: синуса, косинуса, тангенса и котангенса; а также обратных к ним функций: арксинуса, арккосинуса, арктангенса и арккотангенса. 
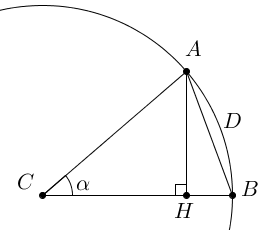Доказательство неравенства |sin α| ≤ |α|.
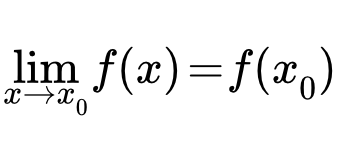Приводятся определения и формулировки основных теорем и свойств непрерывной функции одной переменной. Рассмотрены свойства непрерывной функции в точке, на отрезке, предел и непрерывность сложной функции, классификация точек разрыва. Даны определения и теоремы, связанные с обратной функцией. Изложены свойства элементарных функций. Определение непрерывности функции в точке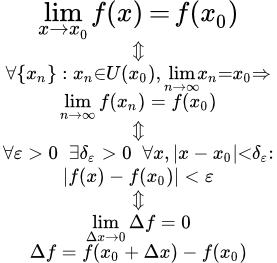Приводится определение непрерывности функции в точке. Рассмотрены эквивалентные определения по Гейне, по Коши и в терминах приращений. Определение односторонней непрерывности на концах отрезка. Формулировка отсутствия непрерывности. Разобраны примеры, в которых требуется доказать непрерывность функции, используя определения по Гейне и по Коши. Свойства непрерывных в точке функций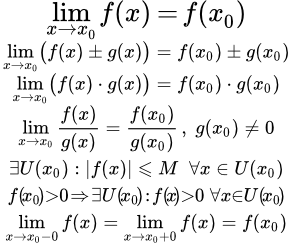Приводятся доказательства основных свойств и теорем, непрерывных в точке функций. Сюда входят: арифметические свойства, теорема об ограниченности, теорема о сохранении знака, свойство односторонней непрерывности. Предел и непрерывность сложной функции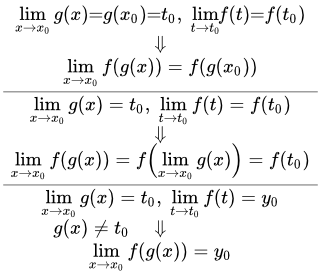Рассмотрены следующие теоремы: теорема о непрерывности сложной функции; теорема о пределе непрерывной функции от функции; теорема о пределе сложной функции. Доказательства этих теорем. Точки разрыва функции – определения, классификация и примерыОпределения точек разрыва первого и второго рода. Основные факты, используемые при исследовании функций на непрерывность. Примеры решения задач, в которых требуется найти точки разрыва и определить вид разрыва. График функции y = 41/(x+2). График заданной функции. Свойства функций, непрерывных на отрезке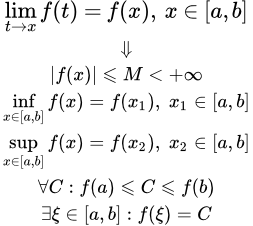Определение и формулировки основных теорем для функций, непрерывных на отрезке. Сюда входят: первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции; вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции; теорема Больцано – Коши о промежуточном значении. Теоремы Вейерштрасса о непрерывных на отрезке функциях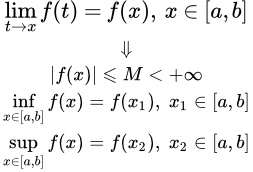Доказательства первой и второй теорем Вейерштрасса об ограниченности и достижении максимума и минимума непрерывной на отрезке функции. Теорема Больцано – Коши о промежуточном значении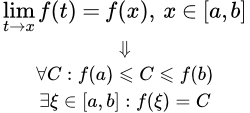Формулировка и доказательство теоремы Больцано – Коши о промежуточном значении функции, непрерывной на отрезке . Обратные функции – определение и свойстваОпределение обратной функции и ее свойства: теорема о взаимной монотонности прямой и обратной функций; симметрия графиков прямой и обратной функций; теоремы о существовании и непрерывности обратной функции для функции, строго монотонной на отрезке, интервале и полуинтервале. Примеры обратных функций. Пример решения задачи. Графики y = sin x и обратной функции y = arcsin x. Графики y = 2x и обратной функции y = log2 x. 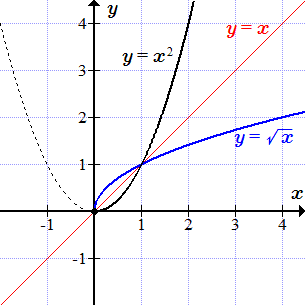Графики y = x2 и обратной функции y = √x. Теорема о существовании и монотонности обратной функции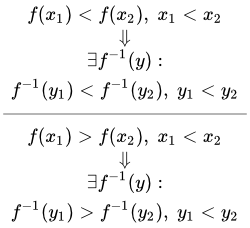Формулировка и доказательство теоремы о существовании и монотонности обратной функции. График обратной функции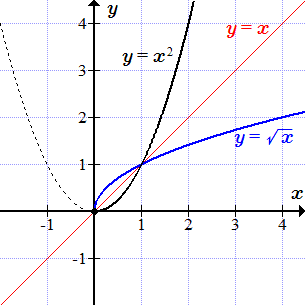Доказательство свойства симметрии графиков прямой и обратной функций. Примеры графиков прямых и обратных функций: параболы и корни, степенные функция и логарифмы, тригонометрические функции и обратные к ним. Применение операции сужения функции. График обратной функции y = f –1(x) симметричен графику прямой функции y = f(x) относительно прямой y = x. График кубической параболы y = x3 и обратной функции – кубического корня y = √3x. График показательной функции с основанием 2, y = 2x и обратной функции – логарифма с основанием 2, y = log2 x. График экспоненты y = ex и обратной функции – натурального логарифма y = ln x. График синуса y = sin x и обратной функции – арксинуса y = arcsin x. График косинуса y = cos x и обратной функции – арккосинуса y = arccos x. График тангенса y = tg x и обратной функции – арктангенса y = arctg x. График котангенса y = ctg x и обратной функции – арккотангенса y = arcctg x. Теоремы о существовании и непрерывности обратной функции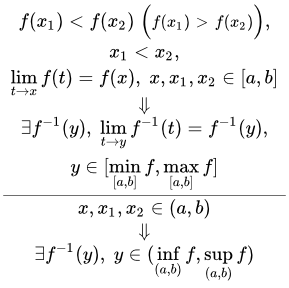Доказательство теорем о существовании и непрерывности обратной функции. Рассмотрены три теоремы для строго монотонной функции на отрезке, интервале и полуинтервале. Для любого ε > 0 существует δ, так что |f -1(y) – f -1(y0)| < ε для всех |y – y0| < δ. Для любого ε > 0 существует δ, так что f -1(y) – f -1(m) < ε для всех y – a < δ. Для любого ε > 0 существует δ, так что f -1(M) – f -1(y) < ε для всех M – y < δ. Неравенства и лемма Бернулли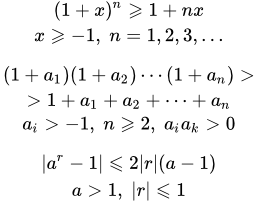Дано неравенство Бернулли и его следствие, которое называется леммой Бернулли. Неравенство приводится в двух формах. Приводятся доказательства неравенств и леммы. Определение и свойства показательной функции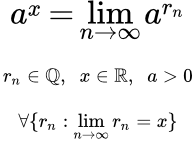Определение и свойства показательной функции на множестве натуральных, целых и рациональных чисел. Определение на множестве действительных чисел посредством предела последовательности. Теорема о свойствах показательной функции. Свойства показательной функции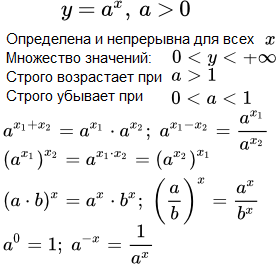Доказательство теоремы о свойствах показательной функции на множестве действительных чисел. Свойства включают: область определения, множество значений, непрерывность, формулы с показательной функцией. Определение и доказательство свойств логарифма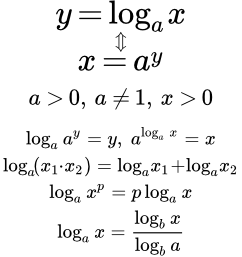Дано определение логарифма с основанием a как функции, обратной к показательной. Основываясь на свойствах показательной функции и теореме об обратной функции, дается вывод свойств логарифма. Непрерывность и свойства степенной функции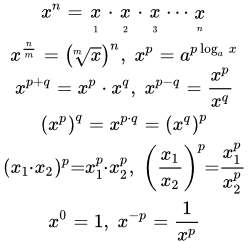Дано определение степенной функции. Показано, что ее можно представить как сложную, составленную из логарифмической и показательной функций. Основываясь на их свойствах, дается доказательство непрерывности и вывод свойств степенной функции. Графики степенной функции y = x p при различных значениях показателя p. Доказательство непрерывности тригонометрических функций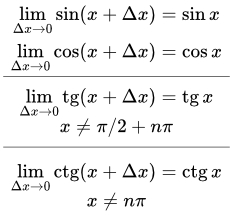Дано доказательство непрерывности тригонометрических функций: синуса, косинуса, тангенса и котангенса; а также обратных к ним функций: арксинуса, арккосинуса, арктангенса и арккотангенса. Доказательство неравенства |sin α| ≤ |α|.