Производные элементарных функций. Доказательство теоремы

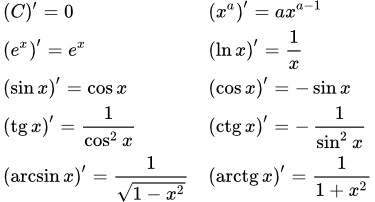
Теорема. Производные элементарных функций

Элементарные функции, перечисленные ниже, каждая на своей области определения, имеют производные, которые определяются по приведенным ниже формулам.
1) , где C – постоянная, ; ⇓
2) ; ⇓
3) ; ⇓
4.1) ; ⇓
4.2) ; ⇓
5.1) ; ⇓
5.2) ; ⇓
6) ; ⇓
7) ; ⇓
8) ; ⇓
9) ; ⇓
10) ; ⇓
11) ; ⇓
12) ; ⇓
13) ; ⇓
14) ; ⇓
15) ; ⇓
16) . ⇓

Доказательство

Все, что нам требуется сделать – это вычислить предел:
(1)   ,
где – одна из элементарных функций. Заметим, что функция за знаком предела зависит от двух переменных, x и Δx:
(2)   .
Сама элементарная функция и ее производная зависят только от одной переменной x. Функция , определяемая по формуле (2), зависит от двух переменных. Но при вычислении производной, мы считаем, что переменная x принимает произвольное фиксированное значение, принадлежащее области определения функции. То есть мы считаем, что x является постоянной. Таким образом мы вычисляем предел от функции одной переменной:
(3)   , где .

Для вычислений таких пределов нам нужно знать свойства элементарных функций. Они приводятся в разделе «Основные элементарные функции и их свойства». Доказательство свойств приводится в разделе «Непрерывность функций». Также нам нужно уметь вычислять пределы. Применяемые при этом методы изложены в разделе «Методы вычисления пределов функций и раскрытия неопределенностей». И наконец, нужно знать правила вычисления производных. См. «Правила дифференцирования».

1) Производная постоянной функции

Докажем, что производная постоянной функции равна нулю:
, где C – постоянная, .
Пусть – постоянная функция. Ее значения определены для всех x и не зависят от переменной x. Поэтому
, при .
Таким образом, функция определена для всех значений переменной , кроме точки . Она является постоянной, равной нулю, , на всей области определения – то есть в любой проколотой окрестности точки . Тогда согласно теореме о пределе постоянной функции,
.

2) Производная показательной функции

Докажем, что производная показательной функции пропорциональна самой функции:
.

Воспользуемся свойствами показательной функции:
.
Применим следствие второго замечательного предела, согласно которому :
.
Здесь мы также воспользовались арифметическими свойствами предела функции.

3) Производная экспоненты

Докажем, что производная экспоненты равна самой экспоненте:
.

Для доказательства, подставим в формулу производной показательной функции, значение основания степени, равного числу e. Также воспользуемся тем, что :
.

Среди всех показательных функций (с различными значениями основания a), производная экспоненты имеет наиболее простой вид. Многие вычисления в математическом анализе оказываются более простыми, если в качестве основания показательной функции использовать число e. Поэтому в математическом анализе, показательную функцию стремятся привести к основанию e, то есть к экспоненте.

4.1) Производная логарифма

Докажем, что
.

Воспользуемся свойствами логарифма:
.
Преобразуем отношение приращения функции к приращению ее аргумента:
.
Сделаем подстановку , и применим следствие второго замечательного предела, согласно которому   :

.
Здесь мы также воспользовались арифметическими свойствами предела функции.

4.2) Производная логарифма модуля

Докажем часто используемую формулу:
.

Рассмотрим функцию как сложную, составленную из двух функций:
.
Найдем производную модуля x.
При .
При .
Тогда .
Применяем формулу производной сложной функции:
.

5) Производная натурального логарифма

Натуральный логарифм – это логарифм с основанием, равным числу e. Подставляя в формулы 4.1) и 4.2) a=e, имеем:
;
.

6) Производная степенной функции

Докажем, что
.

Для доказательства, представим степенную функцию как сложную, составленную из экспоненты и натурального логарифма:
;
или .
Применяем правило дифференцирования сложной функции:

.
Здесь мы воспользовались свойствами степенной функции и правилом вынесения постоянной за знак производной, согласно которому .

7) Производная степенной функции с натуральным показателем степени

В предыдущем пункте мы считали, что показатель степени a является действительным числом, а переменная x больше нуля. Но если a является натуральным (), то степенная функция определена для всех действительных x. Докажем, что и в этом случае, производная степенной функции определяется по той же формуле, что и для действительных значений показателя степени:
.
Случай линейной функции с рассмотрен ниже, поскольку при и , приведенная формула приводит к неопределенному значению .

Пусть . Используем формулу бинома Ньютона:
.
Тогда ,
где .


.

Выше мы предполагали, что . Теперь рассмотрим случай .

.

Таким образом и при , и при , производная определяется по одной и той же формуле: .

8) Производная линейной функции

Докажем, что производная линейной функции равна единице:
.

.
Функция определена для всех значений аргумента, кроме точки . При , , то есть является постоянной. Применяем теорему о пределе постоянной функции:
.

9) Производные синуса и косинуса

Докажем, что производная синуса равна косинусу:
.

Преобразуем приращение функции синус, применяя формулы тригонометрии:
;

.
Выписываем отношение приращения функции синус к приращению ее аргумента и выполняем преобразования:

.
Применяем арифметические свойства предела функции и первый замечательный предел:

.

Аналогичным образом докажем, что производная косинуса равна минус синусу:
.

;

;

;


.

10) Производные тангенса и котангенса

Докажем формулы производных тангенса и котангенса:
.
Для доказательства выразим эти функции через синус и косинус (см. «Тангенс и котангенс – свойства, графики, формулы»). Далее применим формулу производной дроби.

При имеем:

.

При имеем:

.

11) Производные арксинуса и арккосинуса

Докажем формулу производной арксинуса:
.

Арксинус является функцией, обратной к синусу. При   и   имеют место следующие соотношения (см. «Арксинус, арккосинус – свойства, графики, формулы»):
.
Производную синуса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Отсюда . Поскольку при ,   , то
. Тогда
.

Аналогичным способом докажем формулу производной арккосинуса:
.

При   и   имеем:
;
;
.
Поскольку при ,   , то
. Тогда
.

Заметим, что формулу для арккосинуса можно было доказать, используя формулу:
.

12) Производные арктангенса и арктангенса

Докажем формулу производной арктангенса:
.

Арктангенс является функцией, обратной к тангенсу. При   и   имеют место следующие соотношения (см. «Арктангенс, арккотангенс – свойства, графики, формулы»):
.
Производную тангенса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Тогда
;
.

Аналогичным способом докажем формулу производной арккотангенса:
.

При   и   имеем:
;
;
;

;
.

Формулу для арккотангенса также можно доказать, используя соотношение:
.

13) Производные гиперболического синуса и гиперболического косинуса

Докажем, что производная гиперболического синуса равна гиперболическому косинусу:
.

Согласно определению гиперболического синуса,
.
Применяем правила дифференцирования:

.

Аналогичным образом доказываем, что производная гиперболического косинуса равна гиперболическому синусу:
.

Согласно определению гиперболического косинуса,
.
Применяем правила дифференцирования:

.

14) Производные гиперболического тангенса и гиперболического котангенса

Докажем формулы производных гиперболического тангенса и гиперболического котангенса:
.
Для доказательства выразим эти функции через гиперболические синус и косинус (см. «Определения гиперболических функций»), и применим формулу производной дроби.

.

При имеем:

.

15) Производные гиперболического арксинуса и гиперболического арккосинуса

Докажем формулу производной гиперболического арксинуса:
.

Для этого воспользуемся свойствами обратных гиперболических функций. Для действительных x и y имеют место следующие соотношения:
.
Производную гиперболического синуса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Отсюда . Поскольку , то
. Тогда
.

Аналогичным способом докажем формулу производной гиперболического арккосинуса:
.

При   и   имеем:
;
;
.
Поскольку при ,   , то
. Тогда
.

16) Производные гиперболического арктангенса и гиперболического арктангенса

Докажем формулу производной гиперболического арктангенса:
.

Гиперболический арктангенс является функцией, обратной к гиперболическому тангенсу. При   и   имеют место следующие соотношения (см. «Обратные гиперболические функции, их графики и формулы»):
.
Производную гиперболического тангенса мы знаем:
.
Применяем теорему о производной обратной функции:
.
Используем соотношение: . Тогда
;
.

Аналогичным способом докажем формулу производной гиперболического арккотангенса:
.

При   и   имеем:
;
;
;

;
.

Теорема доказана.