Производная дроби из двух функций
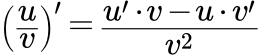
Формула производной дроби
Пусть функции и определены в некоторой окрестности точки и имеют в точке производные. И пусть . Тогда их частное имеет в точке производную, которая определяется по формуле:
(1) .
Доказательство
Введем обозначения:
;
.
Здесь и являются функциями от переменных и . Но для простоты записи мы будем опускать обозначения их аргументов.
Далее замечаем, что
;
.
По условию функции и имеют производные в точке , которые являются следующими пределами:
;
.
Из существования производных следует, что функции и непрерывны в точке . Поэтому
;
.
Рассмотрим функцию y от переменной x, которая является дробью из функций и :
.
Рассмотрим приращение этой функции в точке :
.
Умножим на :
.
Отсюда
.
Теперь находим производную:
.
Итак,
.
Формула доказана.
Вместо переменной можно использовать любую другую переменную. Обозначим ее как x. Тогда если существуют производные и , причем , то производная дроби, составленной двух функций, определяется по формуле:
.
Или в более короткой записи
(1) .
Доказательство вторым способом
Рассмотрим уравнение
.
Здесь , и есть функции от переменной x.
Умножим на :
.
Дифференцируем по переменной x, применяя формулу производной произведения двух функций:
.
Отсюда находим искомую производную:
;
.
Примеры
Все примеры Здесь мы рассмотрим простые примеры вычисления производной дроби, применяя формулу производной частного (1). Заметим, что в более сложных случаях, находить производную дроби проще с помощью логарифмической производной.
Ниже рассмотрены следующие примеры вычисления производных:
Пример 1
Все примеры Найдите производную дроби
,
где , , , – постоянные.
Решение
Применим правило дифференцирования суммы функций:
.
Производная постоянной
.
Из таблицы производных находим:
.
Тогда
;
.
Заменим на и на :
.
Теперь находим производную дроби по формуле
.
.
Ответ
.
Пример 2
Все примеры Найти производную функции от переменной x
.
Решение
Применяем правила дифференцирования, как в предыдущем примере.
;
.
Применяем правило дифференцирования дроби
.
.
Раскрываем скобки.
.
Ответ
.
Пример 3
Все примеры Найти производную дроби
.
Решение
Из таблицы производных находим:
.
Применяем правила дифференцирования суммы и постоянной.
;
.
Применяем формулу для производной дроби:
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
