Теорема о производной обратной функции
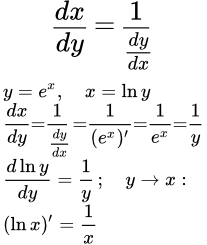
Теорема
Пусть функция
(1)
непрерывна и строго монотонна в некоторой окрестности точки . И пусть в этой точке существует отличная от нуля производная . Тогда обратная функция
(2)
имеет в точке производную, равную обратной величине производной исходной функции:
(3) .
Разумеется, можно использовать любые обозначения для переменных. Так, вместо (3) можно написать так:
.
При этом функция должна быть непрерывной и строго монотонной в окрестности точки x. Формулу (3) можно записать через дифференциалы. Тогда она примет наиболее простой вид:
(4) .
Доказательство
1. Поскольку функция непрерывна и строго монотонна в некоторой окрестности точки , то согласно теореме о существовании и непрерывности обратной функции на интервале, существует такая окрестность точки , на которой определена обратная функция , которая непрерывна и строго монотонна на этой окрестности.
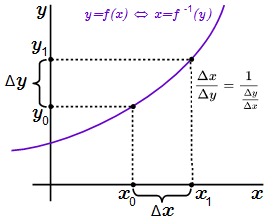
2. Возьмем точку , расположенную в рассматриваемой окрестности . Ее образ обозначим как . Вводим новые переменные и , называемые приращениями переменных: . Выпишем все используемые обозначения, связанные с отображением точек и функцией f и обратной к ней функции f–1:
(5) ;
(6) .
Используем очевидное алгебраическое соотношение:
(7) .
Как отмечено, оно выполняется при и . Преобразуем отношение приращения обратной функции к приращению ее аргумента, используя (7) и обозначения (5) и (6):
.
Итак, мы получили следующее алгебраическое соотношение:
(8) .
3. Теперь выполним предельный переход . Для этого мы намерены применить теорему о пределе сложной функции. Поэтому представим выражение в левой части (8) как сложную функцию.
Считаем, что и являются фиксированными числами. Нам нужно найти предел при от следующей функции, зависящей от переменной :
(9) .
Мы обозначили ее как . Тогда уравнение (8) можно рассматривать как эту же функцию, выраженную через переменную . Обозначим ее как :
(10) .
Сюда нужно еще добавить отображение, связывающее переменные и . Такое отображение мы обозначим как :
(11) .
Тогда функцию p можно рассматривать как сложную:
(12) .
Можно непосредственно убедиться в справедливости (12). Для этого подставим (11) в (10):
.
Выполняем преобразования, используя (5), (6) и (11):
;
;
.
Все верно.
4. Теперь применяем теорему о пределе сложной функции. к пределу
,
где
(9) ;
(10) ;
(11) .
1) Как было указано в самом начале доказательства, обратная функция определена и непрерывна в некоторой окрестности точки . Тогда согласно определению непрерывности функции в точке в терминах приращений,
(13) .
2) Теперь нам нужно показать, что существует такая проколотая окрестность точки , в которой .
Рассмотрим точку . Из (6) следует, что при этом . Действительно, тогда . Поскольку, как было указано в самом начале доказательства, обратная функция строго монотонна, то она принимает значение только в одной точке . Следовательно, переменная принимает нулевое значение только в одной точке, в которой . Поэтому
(14) если , то и .
3) Находим предел от при . Предел в знаменателе равен производной функции f в точке , которая существует по условию теоремы:
.
По условию, . Применяем арифметические свойства предела функции:
.
Все предварительные вычисления и условия теоремы о пределе сложной функции выполнены. Находим производную обратной функции:
.
Теорема доказана.
Примеры
Производная натурального логарифма
Рассмотрим экспоненту (экспоненциальную функцию), . Она определена и строго возрастает для всех значений аргумента x. Экспонента имеет производную, равную самой функции: .
Обратной к экспоненте является натуральный логарифм, . Он определен и строго возрастает при положительных значениях аргумента . Найдем его производную, применяя теорему о производной обратной функции.
.
Итак, мы нашли производную натурального логарифма, выраженную через переменную y:
.
Переменные мы можем обозначать любыми буквами. Поэтому, поменяем y на x:
.
Производная арксинуса
Рассмотрим функцию синус, . Синус строго возрастает при . Поэтому на этом интервале определена обратная функция, которая называется арксинусом, . См. «Доказательство непрерывности тригонометрических функций»
Находим производную арксинуса, применяя теорему о производной обратной функции.
.
Итак, мы получили:
.
Теперь нужно выразить правую часть через переменную . Поскольку при , то . Тогда
.
Наконец, заменив переменную y на букву x, получаем формулу производной арксинуса, записанную в привычном виде:
.
Автор: Олег Одинцов. Опубликовано:
