Сложное движение точки. Пример решения задачи
Теория, применяемая для решения приведенной ниже задачи, излагается на странице “Сложное движение точки, теорема Кориолиса”.
Условие задачи

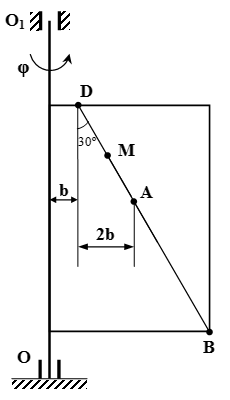
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6t 2 – 3t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40(t – 2t 3) – 40 (s - в сантиметрах, t - в секундах). Расстояние b = 20 см. На рисунке точка M показана в положении, при котором s = AM > 0 (при s < 0 точка M находится по другую сторону от точки A).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с.
Указания. Эта задача – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений (теорема Кориолиса). Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени t 1 = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунке к задаче).
Решение задачи
Дано: b = 20 см, φ = 6t 2 – 3t3, s = |AM| = 40(t – 2t3) – 40, t1 = 1 c.
Найти: vабс, aабсОпределение положения точки
Определяем положение точки в момент времени t = t1 = 1 c.
s = 40(t1 – 2t13) – 40 = 40(1 – 2·13) – 40 = –80 см.
Поскольку s < 0, то точка M ближе к точке B, чем к D.
|AM| = |–80| = 80 см.
Делаем рисунок.
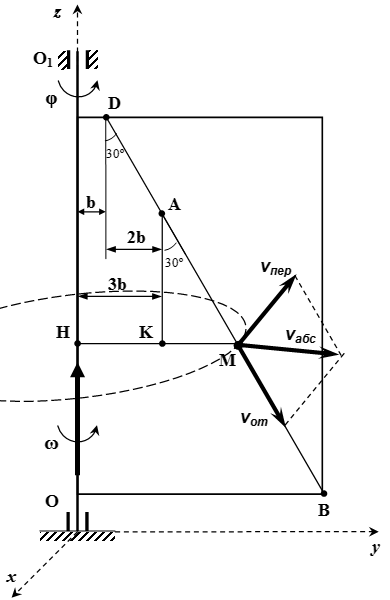
Определение абсолютной скорости точки
Согласно теореме о сложении скоростей, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Определение относительной скорости точки
Определяем относительную скорость . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD. Дифференцируя s по времени t, находим проекцию скорости на направление BD:
.
В момент времени t = t1 = 1 с,
см/с.
Поскольку , то вектор направлен в направлении, противоположном BD. То есть от точки M к точке B. Модуль относительной скорости
vот = 200 см/с.
Изображаем вектор на рисунке.
Определение переносной скорости точки
Определяем переносную скорость . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO1. Дифференцируя φ по времени t, находим угловую скорость вращения пластины:
.
В момент времени t = t1 = 1 с,
.
Поскольку , то вектор угловой скорости направлен в сторону положительного угла поворота φ, то есть от точки O к точке O1. Модуль угловой скорости:
ω = 3 с-1.
Изображаем вектор угловой скорости пластины на рисунке.
Из точки M опустим перпендикуляр HM на ось OO1.
При переносном движении точка M движется по окружности радиуса |HM| с центром в точке H.
|HM| = |HK| + |KM| = 3b + |AM| sin 30° = 60 + 80·0,5 = 100 см;
Переносная скорость:
vпер = ω|HM| = 3·100 = 300 см/с.
Вектор направлен по касательной к окружности в сторону вращения.
Определение абсолютной скорости точки
Определяем абсолютную скорость . Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Проводим оси неподвижной системы координат Oxyz . Ось z направим вдоль оси вращения пластины. Пусть в рассматриваемый момент времени ось x перпендикулярна пластине, ось y лежит в плоскости пластины. Тогда вектор относительной скорости лежит в плоскости yz . Вектор переносной скорости направлен противоположно оси x . Поскольку вектор перпендикулярен вектору , то по теореме Пифагора, модуль абсолютной скорости:
.
Определение абсолютного ускорения точки
Согласно теореме о сложении ускорений (теорема Кориолиса), абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.
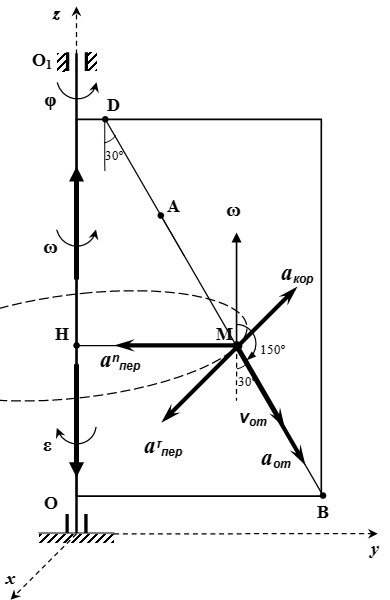
Определение относительного ускорения
Определяем относительное ускорение . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD. Дважды дифференцируя s по времени t, находим проекцию ускорения на направление BD:
.
В момент времени t = t1 = 1 с,
см/с2.
Поскольку , то вектор направлен в направлении, противоположном BD. То есть от точки M к точке B. Модуль относительного ускорения
aот = 480 см/с2.
Изображаем вектор на рисунке.
Определение переносного ускорения
Определяем переносное ускорение . При переносном движении точка M жестко связана с пластиной, то есть движется по окружности радиуса |HM| с центром в точке H. Разложим переносное ускорение на касательное к окружности и нормальное ускорения:
.
Дважды дифференцируя φ по времени t, находим проекцию углового ускорения пластины на ось OO1:
.
В момент времени t = t1 = 1 с,
с –2.
Поскольку , то вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ, то есть от точки O1 к точке O. Модуль углового ускорения:
ε = 6 с-2.
Изображаем вектор углового ускорения пластины на рисунке.
Переносное касательное ускорение:
aτпер = ε |HM| = 6·100 = 600 см/с2.
Вектор направлен по касательной к окружности. Поскольку вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ, то направлен в сторону, противоположную положительному направлению поворота φ . То есть направлен в сторону оси x .
Переносное нормальное ускорение:
anпер = ω2 |HM| = 32·100 = 900 см/с2.
Вектор направлен к центру окружности. То есть в сторону, противоположную оси y .
Определение кориолисова ускорения
Кориолисово (поворотное) ускорение:
.
Вектор угловой скорости направлен вдоль оси z . Вектор относительной скорости направлен вдоль прямой |DB|. Угол между этими векторами равен 150° . По свойству векторного произведения,
.
Направление вектора определяется по правилу буравчика. Если ручку буравчика повернуть из положения в положение , то винт буравчика переместится в направлении, противоположном оси x .
Определение абсолютного ускорения
Абсолютное ускорение:
.
Спроектируем это векторное уравнение на оси xyz системы координат.
;
;
.
Модуль абсолютного ускорения:
.
Ответ
Абсолютная скорость ;
абсолютное ускорение .
Автор: Олег Одинцов. Опубликовано:
