Векторный способ задания движения точки
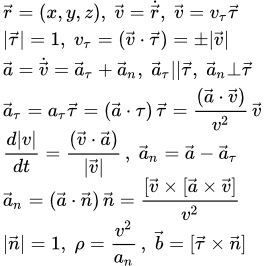
Введение
Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.
Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.
При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
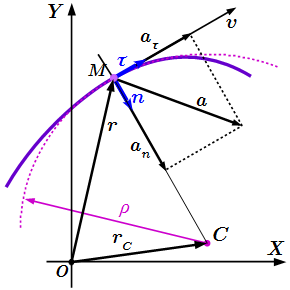
Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.
Нормальное ускорение
Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов. Опубликовано: Изменено:
