Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачи
Порядок решения задач на равновесие с произвольной пространственной системой сил
Чтобы решить задачу на равновесие твердого тела с произвольной пространственной системой сил, надо выбрать прямоугольную систему координат и, относительно нее, составить уравнения равновесия.
Уравнения равновесия, для произвольной системы сил, распределенных в трехмерном пространстве, представляют собой два векторных уравнения:
векторная сумма сил, действующих на тело, равна нулю
(1) ;
векторная сумма моментов сил, относительно начала координат, равна нулю
(2) .
Пусть Oxyz – выбранная нами система координат. Спроектировав уравнения (1) и (2) на оси этой системы, получим шесть уравнений:
суммы проекций сил на оси xyz равны нулю
(1.x) ;
(1.y) ;
(1.z) ;
суммы моментов сил относительно осей координат равны нулю
(2.x) ;
(2.y) ;
(2.z) .
Здесь мы считаем, что на тело действуют n сил, включая силы реакций опор.
Пусть произвольная сила , с компонентами , приложена к телу в точке . Тогда моменты этой силы относительно осей координат определяются по формулам:
(3.x) ;
(3.y) ;
(3.z) .
Таким образом, порядок решения задачи, на равновесие с произвольной пространственной системой сил, следующий.
- Отбрасываем опоры и заменяем их силами реакций. Если опорой является стержень или нить, то сила реакции направлена вдоль стержня или нити.
- Выбираем прямоугольную систему координат Oxyz.
- Находим проекции векторов сил на оси координат, , и точек их приложения, . Точку приложения силы можно перемещать вдоль прямой, проведенной через вектор силы. От такого перемещения значения моментов не изменятся. Поэтому выбираем наиболее удобные для расчета точки приложения сил.
- Составляем три уравнения равновесия для сил (1.x,y,z).
- Для каждой силы, по формулам (3.x,y,z), находим проекции моментов силы на оси координат.
- Составляем три уравнения равновесия для моментов сил (2.x,y,z).
- Если число переменных больше числа уравнений, то задача статически неопределима. Методами статики ее решить нельзя. Нужно использовать методы сопротивления материалов.
- Решаем полученные уравнения.
Упрощение расчетов
В некоторых случаях удается упростить вычисления, если вместо уравнения (2) использовать эквивалентное условие равновесия.
Сумма моментов сил относительно произвольной оси AA′ равна нулю:
(4) .
То есть можно выбрать несколько дополнительных осей, не совпадающих с осями координат. И относительно этих осей составить уравнения (4).
Далее приводится пример, в котором удается упростить вычисления за счет соответствующего выбора осей.
Пример решения задачи на определение реакций стержней, поддерживающих прямоугольную плиту

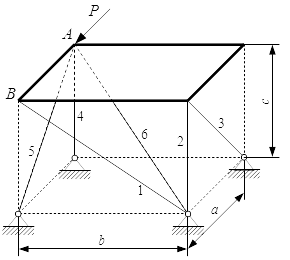
Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве. Система крепления стержней показана на рисунке. На плиту действуют: сила тяжести G; и сила P, приложенная в точке A, направленная вдоль стороны AB.
Дано:
G = 28 kН; P = 35 kН; a = 7,5 м; b = 6,0 м; c = 3,5 м.
Решение задачи
Сначала мы решим эту задачу стандартным способом, применимым для произвольной пространственной системы сил. А затем получим более простое решение, основываясь на конкретной геометрии системы, за счет выбора осей при составлении уравнений равновесия.
Решение задачи стандартным способом
Этот метод хоть и приведет нас к довольно громоздким вычислениям, но он применим для произвольной пространственной системы сил, и может применяться в расчетах на ЭВМ.
Отбросим связи и заменим их силами реакций. Связями здесь являются стержни 1–6. Вводим вместо них силы , направленные вдоль стержней. Направления сил выбираем наугад. Если мы не угадаем с направлением какой-либо силы, то получим для нее отрицательное значение.
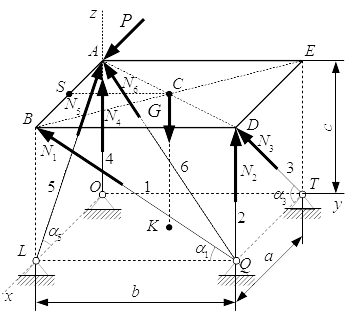
Проводим систему координат Oxyz с началом в точке O.
Находим проекции сил на оси координат.
Для силы имеем:
.
Здесь α1 – угол между LQ и BQ. Из прямоугольного треугольника LQB:
м;
;
.
Силы , и параллельны оси z. Их компоненты:
;
;
.
Для силы находим:
.
Здесь α3 – угол между QT и DT. Из прямоугольного треугольника QTD:
м;
;
.
Для силы :
.
Здесь α5 – угол между LO и LA. Из прямоугольного треугольника LOA:
м;
;
.
Сила направлена по диагонали прямоугольного параллелепипеда. Она имеет следующие проекции на оси координат:
.
Здесь – направляющие косинусы диагонали AQ:
м;
;
;
.
Выбираем точки приложения сил. Воспользуемся тем, что их можно перемещать вдоль линий, проведенных через векторы сил. Так, в качестве точки приложения силы можно взять любую точку на прямой TD. Возьмем точку T, поскольку для нее x и z - координаты равны нулю:
.
Аналогичным способом выбираем точки приложения остальных сил.
В результате получаем следующие значения компонентов сил и точек их приложений:
; (точка B);
; (точка Q);
; (точка T);
; (точка O);
; (точка A);
; (точка A);
; (точка A);
; (точка K).
Составляем уравнения равновесия для сил. Суммы проекций сил на оси координат равны нулю.
;
;
.
Находим проекции моментов сил на оси координат.
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
Составляем уравнения равновесия для моментов сил. Суммы моментов сил относительно осей координат равны нулю.
;
;
;
Итак, мы получили следующую систему уравнений:
(П1) ;
(П2) ;
(П3) ;
(П4) ;
(П5) ;
(П6) .
В этой системе шесть уравнений и шесть неизвестных. Далее сюда можно подставить численные значения и получить решение системы, используя математическую программу вычисления системы линейных уравнений.
Но, для этой задачи, можно получить решение без использования средств вычислительной техники.
Эффективный способ решения задачи
Мы воспользуемся тем, что уравнения равновесия можно составлять не единственным способом. Можно произвольным образом выбирать систему координат и оси, относительно которых вычисляются моменты. Иногда, за счет выбора осей, можно получить уравнения, которые решаются более просто.
Воспользуемся тем, что, в равновесии, сумма моментов сил относительно любой оси равна нулю. Возьмем ось AD. Сумма моментов сил относительно этой оси равна нулю:
(П7) .
Далее заметим, что все силы, кроме пересекают эту ось. Поэтому их моменты равны нулю. Не пересекает ось AD только одна сила . Она также не параллельна этой оси. Поэтому, чтобы выполнялось уравнение (П7), сила N1 должна равняться нулю:
N1 = 0.
Теперь возьмем ось AQ. Сумма моментов сил относительно нее равна нулю:
(П8) .
Эту ось пересекают все силы, кроме . Поскольку сила не параллельна этой оси, то для выполнения уравнения (П8) необходимо, чтобы
N3 = 0.
Теперь возьмем ось AB. Сумма моментов сил относительно нее равна нулю:
(П9) .
Эту ось пересекают все силы, кроме , и . Но N3 = 0. Поэтому
.
Момент от силы относительно оси равен произведению плеча силы на величину проекции силы на плоскость, перпендикулярную оси. Плечо равно минимальному расстоянию между осью и прямой, проведенной через вектор силы. Если закручивание происходит в положительном направлении, то момент положителен. Если в отрицательном – то отрицательный. Тогда
.
Отсюда
kН.
Остальные силы найдем из уравнений (П1), (П2) и (П3). Из уравнения (П2):
N6 = 0.
Из уравнений (П1) и (П3):
kН;
kН
Таким образом, решая задачу вторым способом, мы использовали следующие уравнения равновесия:
;
;
;
;
;
.
В результате мы избежали громоздких расчетов, связанных с вычислениями моментов сил относительно осей координат и получили линейную систему уравнений с диагональной матрицей коэффициентов, которая сразу разрешилась.
Ответ
N1 = 0; N2 = 14,0 kН; N3 = 0; N4 = -2,3 kН; N5 = 38,6 kН; N6 = 0;
Знак минус указывает на то, что сила N4 направлена в сторону, противоположную той, которая указана на рисунке.
Автор: Олег Одинцов. Опубликовано:
