Линейные дифференциальные уравнения в частных производных первого порядка

Представлены способы решения линейных однородных и неоднородных дифференциальных уравнений в частных производных первого порядка методом характеристик. Даны примеры решения таких задач. В разобранных примерах получено общее решение заданного уравнения. На его основе найдено частное решение, удовлетворяющее заданным граничным условиям.

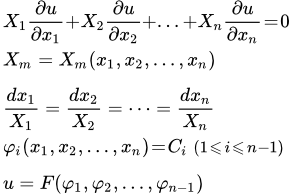
Линейные однородные уравнения в частных производных первого порядка

Пусть X₁, X₂, ..., X_n – заданные функции переменных x₁, x₂, ..., x_n .

Чтобы решить линейное однородное уравнение в частных производных первого порядка:
X₁ ∂u∂x₁  + X₂ ∂u∂x₂  + ... + X_n ∂u∂x_n  = 0
необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
dx₁ X₁  = dx₂ X₂  =  ...   = dx_n X_n   : 
Далее нужно представить решение в виде:
φ₁(x₁, x₂, ..., x_n ) = C₁ ,
φ₂(x₁, x₂, ..., x_n ) = C₂ ,
..................
φ_n-1(x₁, x₂, ..., x_n ) = C_n-1 ,
где C_k – постоянные.
После чего сразу получаем общее решение:
u = F (φ₁ , φ₂ , ..., φ_n – 1 )  , 
где F – произвольная функция от n – 1 аргументов.

Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .

Линейные неоднородные уравнения в частных производных первого порядка

Пусть X₁, X₂, ..., X_n+1 – заданные функции от переменных x₁, x₂, ..., x_n и z .

Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
X₁ ∂z∂x₁  + X₂ ∂z∂x₂  + ... + X_n ∂z∂x_n  = X_n + 1  , 
необходимо решить уравнение характеристик:
dx₁ X₁  = dx₂ X₂  =  ...   = dx_n X_n  = dzX_n + 1   . 
Решение этой системы нужно представить в следующем виде:
φ₁(x₁, x₂, ..., x_n , z ) = C₁ ,
φ₂(x₁, x₂, ..., x_n , z ) = C₂ ,
..................
φ_n(x₁, x₂, ..., x_n , z ) = C_n .
После чего сразу получаем общий интеграл в неявном виде:
F (φ₁ , φ₂ , ..., φ_n )  = 0
где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ₁ = F(φ₂, φ₃, ..., φ_n) ,
φ₂ = F(φ₁, φ₃, ..., φ_n) ,
и т. д.

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
x ∂u∂x – 12 y ∂u∂y +  (z + x⁴ y² ) ∂u∂z = 0 , 
u = 2z – x² 2x²    при  xy = – 1 . 

Решение

Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
dxx = – 2dyy = dzz + x⁴ y²  

Это уравнение характеристик содержит три уравнения:
dxx = – 2dyy  ; 
dxx = dzz + x⁴ y²   ; 
– 2dyy = dzz + x⁴ y²   . 
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.

Выбираем и решаем первое уравнение:
dxx = – 2dyy 
Здесь переменные уже разделены, интегрируем:
∫ dxx = – 2 ∫ dyy 
Интегралы табличные,
ln  | x |  = – 2 ln  | y |  + ln C₁ 
Потенцируем:
C₁  = xy² 
Отсюда
y²  = C₁ x 

Подставим во второе уравнение:
dxx = dzz + x⁴ y²  
dxx = dzz + x⁴ C₁ x  = dzz + C₁ x³  
Или:
dzdx = zx + C₁ x² 
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x ^-1 и преобразуем:
x^– 1 dzdx – x^– 2 z = C₁ x
x^– 1 dzdx + dx^– 1 dx z = C₁ x
ddx (x^– 1 z )  = C₁ x
Интегрируем:
x^– 1 z = C₁ ∫ x dx + C₂  =  C₁ 2 x²  + C₂ 
Подставим полученное ранее выражение C₁ = x y ² :
x^– 1 z = xy² 2 x²  + C₂  = 12 x³ y²  + C₂ 
C₂  = zx – 12 x³ y² 

Итак, мы нашли два интеграла уравнения характеристик:
φ₁  = xy²  = C₁ 
φ₂  = zx – 12 x³ y²  = C₂ 

Общее решение исходного уравнения в частных производных имеет вид:
u = F (φ₁ , φ₂ )  =  F (xy² , zx – 12 x³ y² ) 
где F - произвольная функция от двух аргументов F(φ₁, φ₂) . Найдем ее вид из граничного условия
u = 2z – x² 2x²    при  xy = – 1 . 

Рассматриваем решение на границе.
Положим x y = –1 :
φ₁  = xy²  = (xy ) ² x = (– 1 ) ² x = 1x 
φ₂  = zx – 12 x³ y²  =  zx – 12 x (xy ) ²  = zx – 12 x
Отсюда
x = 1φ₁  
zx²  = φ₂ x + 12 = φ₁ φ₂  + 12 
На границе
u = 2z – x² 2x²  = zx²  – 12 =  φ₁ φ₂  + 12 – 12 = φ₁ φ₂  . 

Итак, мы нашли, что на границе функция F имеет вид:
F(φ₁, φ₂) = φ₁ φ₂ .
Такой же вид она имеет и во всей области
Подставляя
φ₁  = xy²  ; 
φ₂  = zx – 12 x³ y²  , 
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:
u = F (φ₁ , φ₂ )  = φ₁ φ₂  =  xy² ( zx – 12 x³ y²  )  = y² z – 12 x⁴ y⁴ 

Ответ

Общее решение:
u = F (xy² , zx – 12 x³ y² ) 
где F - произвольная функция от двух аргументов F(φ₁, φ₂) .

Частное решение:
u = y² z – 12 x⁴ y⁴ 

Неоднородное уравнение

Найти поверхность, удовлетворяющую данному уравнению
2xz ∂z∂x + 2yz ∂z∂y = z²  – x²  – y²  , 
и проходящую через данную окружность x + y + z = 0 , x² + y² + z² = a² .

Решение

Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
dx2xz = dy2yz = dzz²  – x²  – y²  

Оно содержит три уравнения:
dx2xz = dy2yz  ; 
dy2yz = dzz²  – x²  – y²   ; 
dx2xz = dzz²  – x²  – y²   . 
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.

Решаем уравнение:
dx2xz = dy2yz 
Умножаем на 2 z и интегрируем:
∫ dxx = ∫ dyy 
Интегралы табличные,
ln  | x |  = ln  | y |  + ln C₁ 
Потенцируем:
xy = C₁ 
Отсюда
x = C₁ y

Подставим во второе уравнение:
dy2yz = dzz²  – x²  – y²  
dy2yz = dzz²  – (C₁ y ) ²  – y²  
Или:
z²  – (1 + C²₁ ) y²  = y 2z dzdy 
Замечаем, что 2z dz = d z²  ,  тогда
z²  – (1 + C²₁ ) y²  = y  dz² dy 
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y ² и преобразуем:
dz² dy ⋅ 1y + z²  ⋅ ( – 1y²   )  =  – (1 + C²₁ ) 
ddy ( z² y  )  = – (1 + C²₁ ) 
Интегрируем:
z² y = – (1 + C²₁ ) ∫ dy =  – (1 + C²₁ ) y + C₂ 
Подставим полученное ранее выражение C₁  = xy  и преобразуем:
z² y =  – ( 1 + ( xy  ) ²  ) y + C₂ 
x²  + y²  + z² y = C₂ 

Итак, мы нашли два интеграла уравнения характеристик:
xy = C₁ 
x²  + y²  + z² y = C₂ 

Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:
φ₁  = 2( xy  ) ²  + 2 xy = C₁ 
φ₂  = yx²  + y²  + z²  = C₂ 

Общий интеграл исходного уравнения в частных производных имеет вид:
F(φ₁, φ₂) = 0
Но, поскольку F - произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ₁ = F(φ₂) ,
где F - произвольная функция от одного аргумента.

Найдем вид этой функции, рассматривая решение на границе.
На границе, x ² + y ² + z ² = a ² , φ₂  = ya²   . 
Из уравнения x + y + z = 0 , z = –(x + y) . Подставим в x ² + y ² + z ² = a ² и преобразуем:
x ² + y ² + (x + y) ² = a ²
x ² + y ² + x ² + 2xy + y ² = a ²
2x ² + 2xy + 2y ² = a ²
Разделив на y ² , имеем
φ₁  = 2( xy  ) ²  + 2 xy = a² y²  – 2
Итак, мы нашли, что на границе:
φ₁  = a² y²  – 2
φ₂  = ya²   . 
Подставим в выражение общего интеграла:
φ₁ = F(φ₂)
a² y²  – 2 = F ( ya²   )  . 
Сделаем подстановку
t = ya²  ,  y = a² t  : 
F (t )  = a² y²  – 2 = a² a⁴ t²  – 2 =  1a² t²  – 2 . 

Итак, мы нашли, что на границе функция F имеет вид:
F (t )  = 1a² t²  – 2 . 
Такой же вид она имеет и во всей области, тогда
φ₁  = F (φ₂ )  = 1a² φ²₂  – 2 . 
Подставляем выражения для φ₁ и φ₂ :
φ₁  = 2( xy  ) ²  + 2 xy 
φ₂  = yx²  + y²  + z²  
2( xy  ) ²  + 2 xy =  (x²  + y²  + z² ) ² a² y²  – 2 . 
Умножим на a ²y ² .

Ответ

(x²  + y²  + z² ) ²  =  2a² (x²  + y²  + xy ) 

Автор: Олег Одинцов.     Опубликовано: 23-09-2014