Производная функции в точке – определения, теоремы и свойства
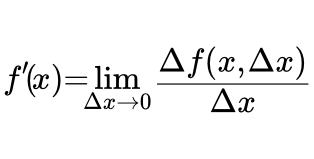
Определение производной
- Производная функции в точке
- Пусть функция f(x) определена в некоторой окрестности точки x0.
Производной функции f(x) в точке x0 называется конечный предел отношения приращения функции к приращению ее аргумента, когда последний стремится к нулю:
(1) .
- Приращение аргумента функции
- в точке – это разность значений аргумента в некоторой точке и точке :
.
Приращение аргумента является независимой переменной. - Приращение функции
- в точке – это разность значений функции в некоторой точке и точке : .
Приращение функции является зависимой переменной. Оно зависит от и , или от и . - Дифференцирование
- – это процесс вычисления производной.
Обозначение производной
Производная функции может обозначаться так:
.
Односторонние производные
- Правая (левая) производная функции f в точке x0
- Пусть функция f(x) определена в правой окрестности точки . Тогда правой производной функции f в точке называется правый предел
.
Соответственно, если функция определена в левой окрестности , то левой производной функции f в точке называется левый предел
.
Правую (левую) производную также называют производной справа (слева) в точке , или правосторонней (левосторонней) производной в точке .
она имеет в этой точке производные справа и слева, и они равны:
.
При этом
.
,
то она не имеет производной в этой точке
Дифференцируемые функции в точке
- Дифференцируемая функция в точке
- Пусть функция f(x) определена в некоторой окрестности точки .
Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде суммы линейной функции от и о-малого по сравнению с :
(1) .
Здесь – действительная величина, зависящая от , но не от ; ;
– о-малое по сравнению с при . То есть
, где .
в этой точке существует производная . При этом
.
Тогда она непрерывна в этой точке.
Тогда в этой точке
(производная суммы функций);
(производная произведения);
, при (производная частного);
(вынесение постоянной за знак производной).
Тогда сложная (составная) функция имеет производную в точке , которая определяется по формуле:
.
Производную сложной функции также можно записать так:
.
Дифференциал функции в точке
Определение
- Дифференциал функции в точке
- Пусть функция дифференцируема в некоторой точке .
Тогда ее приращение в этой точке можно представить в виде суммы линейной функции от приращения ее аргумента и бесконечно малой функции по сравнению с :
.
Дифференциалом функции в точке называется главная линейная часть приращения функции, соответствующая приращению независимой переменной :
.
То есть это приращение функции, в котором опущены слагаемые, содержащие бесконечно малые величины по сравнению с приращением аргумента .
Дифференциал в точке обозначается как или , и является функцией двух переменных: и . Он также называется дифференциалом первого порядка или первым дифференциалом.
- Дифференциал независимой переменной
- – это приращение аргумента функции:
.
Он является независимой переменной.
Дифференциал функции в точке можно записать в одной из следующих форм.
;
;
;
.
Что такое дифференциал функции? В чем суть дифференциала?
Дифференциал функции в точке – это приращение функции в точке, в котором отброшены о - малые функции по сравнению с приращением независимой переменной, при ее стремлении к нулю.
Первый дифференциал функции – это выражение, в котором оставлена только линейная часть приращения независимой переменной.
Также говорят, что
Дифференциалы – это бесконечно малые приращения.
Свойства
Тогда в этой точке
(дифференциал суммы функций);
(дифференциал произведения);
, при (дифференциал частного).
Постоянный множитель можно выносить из-под знака дифференциала:
.
При этом функция имеет производную в точке , а функция имеет производную в точке .
Тогда дифференциал первого порядка функции, выраженный через переменную имеет ту же форму, что и дифференциал, выраженный через переменную :
.
Эту формулу можно записать так:
.
Геометрический смысл производной и дифференциала
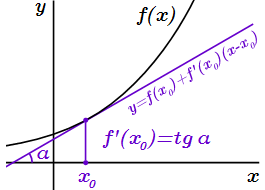
то она равна тангенсу угла между осью абсцисс x и наклонной касательной, проведенной к графику функции в точке . При этом угол считается положительным, если график касательной возрастает; угол отрицательный – если убывает. Другими словами, производная функции в точке равна угловому коэффициенту касательной графика функции в точке , а уравнение касательной имеет вид:
.
2. Если производная функции в точке равна бесконечности: ,
то в этой точке график имеет вертикальную касательную, описываемую уравнением
.
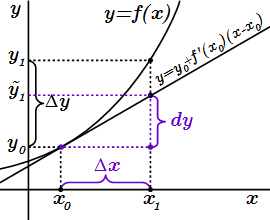
то дифференциал функции в точке – это приращение ординаты касательной, проведенной к графику функции в точке , соответствующее приращению аргумента .
Дифференциал независимой переменной – это приращение аргумента функции: .
Методы вычисления производных
Пусть – функции от ; и пусть они имеют производную в точке ; – постоянная, не зависящая от величина.
Тогда в точке имеют место следующие формулы.
суммы и разности
произведения
формула Лейбница
, при дроби
постоянной
, при
, где сложной функции
обратной функции
; логарифмическая производная
степенно-показательной функции
Пусть . Тогда
производная функции, заданной параметрическим способом
Пусть зависимость от задана уравнением .
Тогда
неявной функции
Производные элементарных функций
Теорема о производных элементарных функций
Далее и являются постоянными.
степенной функции
;
экспоненты и показательной функции
;
; логарифма
синуса
косинуса
тангенса
котангенса
арксинуса и арккосинуса
арктангенса и арккотангенса
Производные и дифференциалы высших порядков
Производные высших порядков
Определение
Поскольку производная сама является функцией от переменной , то можно дать определение производной от производной, которая называется производной второго порядка.
- Производная второго порядка функции
- Пусть для функции , в окрестности некоторой точки , определена ее производная . И пусть имеет производную в этой точке.
Второй производной функции в точке называется производная от первой производной в этой точке:
.
Вторую производную также называют производной второго порядка функции. - Производная n-го порядка функции
- Пусть для функции , в окрестности некоторой точки , определена ее n–1-я производная . И пусть функция имеет производную в этой точке.
n-й производной функции в точке называется производная от n-1-й производной в этой точке:
.
n-ю производную также называют производной n-го порядка функции или производной порядка n функции.
Обозначения
Производная функции второго порядка в точке может обозначаться так:
.
Третьего порядка:
.
Для производных более высоких порядков вместо штрихов используются римские цифры. Например, для четвертого порядка:
.
Для произвольного n-го порядка:
.
При этом стоит иметь в виду, что обозначение является принятым сокращением, под которым подразумевают следующее:
.
Арифметические свойства
Здесь – функции, зависящие от переменной ; – постоянная.
Производная суммы и разности:
.
Вынесение постоянной за знак производной:
.
Производная произведения (формула Лейбница)
.
Производная произведения m функций:
.
Суммирование ведется по всем возможным целым неотрицательным значениям , сумма которых равна n.
Производные высших порядков элементарных функций
показательной функции
натурального логарифма
степенной функции
синуса
косинуса
, где тангенса
, где котангенса
,
где – многочлен степени . Он определяется по формулам:
;
.
Здесь
арксинуса и арккосинуса
арктангенса и арккотангенса
Дифференциалы высших порядков
Определение
- Дифференциал n-го порядка функции в точке
- Пусть функция n раз дифференцируема в точке .
Дифференциалом n-го порядка функции в точке называется дифференциал от дифференциала - го порядка в этой точке при следующих ограничениях.
1. Считается, что дифференциал - го порядка является функцией, зависящей только от одной переменной – аргумента функции . То есть дифференциал независимой переменной рассматривается как постоянная.
2. Приращение аргумента приравнивается к приращению аргумента дифференциала -го порядка.
Дифференциал n-го порядка также называют n-м дифференциалом функции в точке. Он обозначается одним из способов:
,
и определяется по формуле:
(2.4) .
Значение выражения зависит от контекста, в котором оно применяется.
Если оно применяется при вычислении - го дифференциала, то
.
Если это первый дифференциал функции , то
.
Свойства
Дифференциал суммы и разности.
.
Вынесение постоянной за знак дифференциала.
.
Дифференциал произведения двух функций.
.
Дифференциал произведения m функций.
.
Суммирование ведется по всем возможным целым значениям , сумма которых равна n, и каждое из которых заключено в пределах .
Связь дифференциалов с формулой Тейлора
.
Здесь – приращение функции в точке ;
– дифференциал независимой переменной, который по определению является ее приращением.
При этом функции и дифференцируемы n раз в точках и , соответственно.
И пусть n > 1.
Тогда форма дифференциала n - го порядка функции, выраженной через переменную , при n > 1, не совпадает с формой дифференциала этого же порядка, выраженного через переменную :
.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
А.М. Тер-Крикоров, М.И. Шабунин. Курс математического анализа. Москва, ФИЗМАТЛИТ, 2001.
Автор: Олег Одинцов. Опубликовано: Изменено:
