Методы вычисления пределов функций и раскрытия неопределенностей
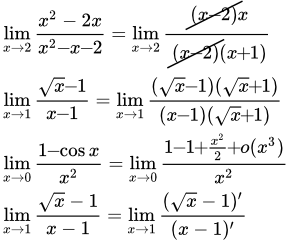
Здесь мы применим теорию к решению задач на вычисление пределов. Теория изложена в разделах «Предел последовательности», «Предел функции» и «Непрерывность функции».
Далее изложены приемы и методы вычисления пределов.
Известные пределы
Пределы с непрерывными функциями
Если функция f непрерывна в конечной точке , то
.
См. «Определение непрерывности». Элементарные функции: , и обратные к ним, непрерывны на своих областях определения.
Пределы с показательной и степенной функциями
Следующие пределы следуют из свойств показательной и степенной функций.
При : , , , .
При : , , , .
При : , , , .
При : , , , .
Замечательные пределы
Первый замечательный предел и его следствия:
; ; ; ; .
См. «Доказательство первого замечательного предела и его следствий», «Примеры решений задач».
Второй замечательный предел и его следствия:
; ; ; ; ; ; ; .
См. «Доказательство второго замечательного предела и его следствий», «Примеры решений задач».
Применение замены переменной
Если функцию можно представить в виде сложной:
,
то можно попытаться упростить процесс вычисления предела , выполняя замену переменной. Для этого мы вычисляем предел
.
Здесь может быть конечным числом , либо одним из символов: .
Если является конечным числом и функция непрерывна в точке , то
.
Если функция не является непрерывной в , то мы должны вычислить предел
.
Если он существует, и при этом существует такая проколотая окрестность точки , на которой
при ,
то существует исходный предел
.
См. «Замена переменной при решении пределов».
Пример.
, .
Арифметические свойства предела функции
Если существуют конечные пределы , , то существуют пределы суммы, разности и произведения функций:
, , .
Если , то существует предел частного:
.
В частности, если C есть постоянная, то
, .
См. «Арифметические свойства предела функции».
Аналогичные свойства имеют место и для бесконечно больших и бесконечно малых функций. Они изложены на странице «Бесконечно малые и бесконечно большие функции». При вычислении таких пределов выполняются следующие правила:
; ;
; ;
; ; ;
;
;
; ; .
Пусть a – произвольное действительное число. Тогда
; ;
; ; ; .
Пусть a > 0. Тогда
; ; .
Пусть a < 0. Тогда
; .
Эти правила применяются следующим образом. Пусть, например , , где – конечное положительное число. Тогда
;
;
;
.
В последнем случае, если это не промежуточное вычисление, можно опустить знак у нуля:
.
Неопределенности
Применение только арифметические свойств пределов не всегда приводит к результату, если в состав исследуемого выражения входят бесконечно большие и бесконечно малые функции. Следующие операции не определены:
; ; ; ;
; ; ;
; ; ; ;
.
Это, так называемые неопределенности. В этих случаях арифметических свойств не достаточно и, для вычисления величины предела, нужно выполнять преобразования, чтобы привести их к известным пределам. Такой процесс называется раскрытием неопределенности.
Выполняя преобразования, можно от неопределенности одного вида переходить к неопределенности другого вида. Последние три неопределенности сводятся к логарифмированием. Например так:
.
То есть мы от неопределенности перешли к . Далее ее можно свести к неопределенностям вида или :
; .
К неопределенности сводится и неопределенность . Покажем это. Пусть и . Тогда
.
Далее излагаются методы раскрытия неопределенностей.
Раскрытие неопределенностей с дробями
При вычислении пределов с дробями, мы используем следующее свойство.
Если значения функции изменить (или сделать неопределенными) в конечном числе точек , то это изменение никак не повлияет на существование и величину предела в произвольной точке .
См. «Влияние значений функции в конечном числе точек на величину предела».
Для примера рассмотрим следующую функцию:
,
где – функция, непрерывная в . Функции f и g отличаются только в одной точке : не определена в этой точке, а – определена и непрерывна. Тогда, согласно приведенному свойству, пределы этих функций в любой точке равны. Поэтому
.
То есть, при вычислении пределов от дробей, числитель и знаменатель можно умножать и делить на конечное число равных сомножителей. В результате таких действий, мы можем получить другую функцию, область определения которой может отличаться от исходной. Но, поскольку это изменение затрагивает только конечное число точек, то это никак не повлияет на существование и величину предела.
Дроби из многочленов
Пусть нам нужно вычислить предел от дроби из многочленов:
.
При , числитель и знаменатель стремятся к бесконечности. Мы имеем неопределенность вида . Для ее раскрытия, разделим числитель и знаменатель на :
.
Далее применяем арифметические свойства пределов функции. Поскольку , то
.
Пусть теперь x стремится к конечному числу x0: x → x0. Если возникает неопределенность вида 0/0, то многочлены в числителе и знаменателе необходимо разделить на x – x0. Например,
.
См. «Решение пределов с дробями из многочленов»
Дроби с корнями
При вычислении пределов дробей с корнями, часто бывают полезными следующие формулы:
,
,
,
. . . . . . . . . . . .
.
Например, пусть требуется вычислить предел
.
При . Мы имеем неопределенность вида . Применим вторую формулу. Подставим :
.
Отсюда
;
;
.
Подобный прием также применяется и для раскрытия некоторых неопределенностей вида . Например:
.
См. «Решение пределов с корнями»
Сравнение функций. О большое и о малое
Говорят, что функция f ограничена относительно функции g при x → x0, пишут
при ,
если функции f и g определены на некоторой проколотой окрестности точки и существует такое число C, что на этой окрестности выполняется неравенство:
.
Здесь . Окрестность может быть как двусторонней, так и односторонней. В последнем случае пишут или .
Функции f и g называются функциями одного порядка при , пишут
при ,
если и при .
Функция α называется бесконечно малой по сравнению с функцией f при , пишут
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Если, в предыдущем определении, f является бесконечно малой функцией при , то говорят, что является бесконечно малой более высокого порядка, чем f при .
Эквивалентные функции
Здесь и далее – конечная или бесконечно удаленная () точка: .
Функции f и g называются эквивалентными (асимптотически равными) при , пишут
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Если, при , , то .
Если, при , и , то .
Если , то при .
Если , то при .
Если на некоторой проколотой окрестности точки ,
и , то
.
Если, при , и и существует предел
, то существует и предел
(э.1) .
В более общем случае, если при , , то
(э.1) .
Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй.
Приводим список часто применяющихся эквивалентных функций при :
;
.
Таким образом применение эквивалентных функций, в ряде случаев, позволяет заменить функцию за знаком предела на более простую и упростить вычисление предела. Подчеркнем, что речь идет только о пределах вида (э.1). Для пределов функций других видов такая замена может привести к ошибкам.
См. «О большое и о малое. Сравнение функций», «Применение эквивалентных функций при решении пределов».
Разложение в степенной ряд
Одним из самых мощных методов раскрытия неопределенности в конечной точке является разложение функций в степенной ряд. Далее приводим разложения элементарных функций при .
;
;
,
где ;
;
;
,
где – числа Бернулли: , ;
;
;
;
;
;
;
;
,
;
;
.
Пример. Пусть нам требуется найти предел
.
Разложим числитель и знаменатель в степенной ряд, в окрестности точки , и находим предел:
;
;
.
См. «Решение пределов, используя ряд Тейлора»
Правило Лопиталя
Теорема о раскрытии неопределенности 0/0
Пусть функции f и g непрерывны и имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точке , причем и не равны нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Теорема о раскрытии неопределенности ∞/∞
Пусть функции f и g непрерывны и имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точке , причем не равна нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Вычислим предыдущий предел, используя правило Лопиталя.
.
См. «Решение пределов, используя правило Лопиталя»
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
