Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил

Рассмотрено решение задачи, в которой материальная точка движется по изогнутой трубе с двумя прямолинейными участками. При этом, кроме силы тяжести и реакций стенок трубы, на первом участке, на точку действует постоянная сила, и сила сопротивления среды, зависящая от скорости; на втором участке – внешняя сила, изменяющаяся со временем.

Здесь мы рассматриваем пример решения задачи на интегрирование дифференциальных уравнений прямолинейного движения материальной точки, находящейся под действием переменных сил. Методы, применяемые при решении задачи, подробно изложены на странице «Интегрирование дифференциальных уравнений прямолинейного движения материальной точки».

Условие задачи

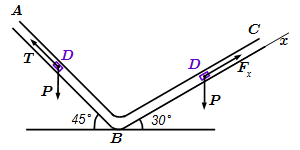
Груз D массой m, получив в точке A начальную скорость V₀, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV², вектор R направлен противоположно скорости V груза).

Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция F_x которой на ось x задана.

Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.

Дано: m = 1,8 кг,   v₀ = 20 м/с,   T = 15 Н,   μ = 0,2 кг/м,   l = 3,0 м,   F_x = 5 – 2sin(3t).

Решение задачи

1. Движение материальной точки на участке AB

1.1. Составление уравнения движения груза

Чтобы найти закон его движения груза D на участке BC, нам нужно найти его скорость в точке B. Для этого рассмотрим движение груза на участке AB; составим уравнение движения; решая которое, определим скорость .

Как сказано в условии, груз можно рассматривать как материальную точку. То есть, считаем, что размерами груза можно пренебречь.

Выберем декартову систему координат с началом в точке A. Направим ось от A к B. Пусть в начальный момент времени , груз находился в точке A.

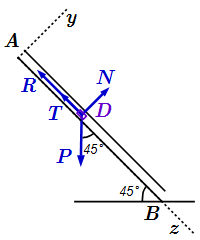
Рассмотрим силы, действующие на груз, и найдем их проекции на ось .
1) Сила тяжести , где м/с² – ускорение свободного падения. Она направлена вертикально вниз и составляет угол с осью . Абсолютное значение силы тяжести: . Проекция на ось :
.
2) Сила . Ее абсолютное значение задано: T = 15 Н. Сила направлена противоположно оси . Поэтому ее проекция на эту ось:
.
3) Сила сопротивления среды по абсолютной величине пропорциональна квадрату скорости: , и направлена противоположно скорости груза. Считаем, что скорость v направлена от A к B. Тогда вектор силы направлен противоположно оси . Его проекция на эту ось:
.
4) Сила давления поверхности . Она перпендикулярна поверхности AB, вдоль которой происходит движения груза. Поэтому ее проекция на ось равна нулю:
.
Если бы на груз действовала сила трения скольжения , то нам нужно было бы определить абсолютное значение силы давления N. Это можно сделать, приравнивая к нулю сумму проекций всех сил на ось Ay: . Но в нашей задаче, значение силы трения скольжения намного меньше величин остальных сил, поэтому мы пренебрегаем ее влиянием на движение.

На участке AB перемещение груза происходит только вдоль оси . Перемещение в перпендикулярных направлениях отсутствует. Поэтому при движении изменяется только координата . Вектор скорости груза также направлен вдоль оси . Поэтому он имеет только одну отличную от нуля компоненту . Тогда . Составляем дифференциальное уравнение движения материальной точки вдоль оси :
.
Подставляем перечисленные выше компоненты внешних сил.
;
(AB.1)   .

1.2. Определение скорости v_B

Выразим вторую производную координаты по времени через скорость . Поскольку , то
.
Подставляем в (AB.1):
(AB.2)   .

Это дифференциальное уравнение первого порядка с разделяющимися переменными. Мы можем его решить, и найти скорость как функцию времени:
(AB.3)   .
Если бы в условии было задано время движения груза на участке AB, то, подставив в (AB.3) значение , мы сразу могли бы получить искомую скорость груза в точке B.

Но у нас известно не время движения по участку AB, а его длина l. Тогда мы можем решить уравнение (AB.2), и получить зависимость . Затем нужно решить уравнение , и получить закон движения груза на участке AB: . Отсюда можно найти значение момента времени , при котором груз окажется в точке B. Зная это время, по формуле (AB.3), можно определить искомое значение скорости в точке B.

Однако есть более простой способ. Он заключается в том, чтобы искать зависимость скорости не от времени, а от координаты: . Для этого в (AB.2) применяем правило дифференцирования сложной функции, учитывая что :
.
Подставим в (AB.2):
.

Разделяем переменные.
(AB.4)   .
Введем постоянную . Тогда (AB.4) примет более простой вид:
;
.
Интегрируем от точки A до точки B:
(AB.5)   .
По условию, скорость в точке A равна : . Обозначим скорость в точке B как . Тогда . Поскольку мы выбрали начало координат в точке A, то . Тогда по условию, . Поставляем в (AB.5):
(AB.6)   .

Интеграл в правой части элементарный:
.

В левой части делаем подстановку :
;

.
Здесь мы учли, что поскольку и , то . Поэтому убрали знак модуля. Также воспользовались свойством логарифма.

Подставляем в (AB.6).
.
Вводим постоянную , и находим :
;
;
;
.

2. Определение закона движения материальной точки на участке BC

2.1. Составление уравнения движения груза

Теперь рассмотрим движение груза D на участке BC. На этом участке мы выберем новую систему координат с началом в точке B, и новый отсчет времени. Ось направим вдоль линии движения груза (см. рисунок). Ось – перпендикулярно. Пусть в момент времени , груз находился в точке B, и, как мы только что нашли, двигался со скоростью .

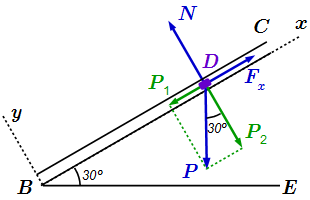
Рассмотрим силы, действующие на груз, и найдем их проекции на ось .
1) Сила тяжести . Она направлена вертикально вниз. Разложим ее по правилу параллелограмма на составляющие и , параллельные осям координат, причем . Поскольку и , то угол между векторами и равен углу между BC и горизонталью BE. Из прямоугольника, образованного векторами , находим: . Тогда проекция силы тяжести на ось равна .
2) Сила . Ее проекция на ось задана в условии задачи: .
3) Сила давления поверхности . Она перпендикулярна поверхности BC. Поэтому ее проекция на ось равна нулю:
.

Составляем дифференциальное уравнение движения материальной точки вдоль оси :
.
Подставляем перечисленные выше компоненты внешних сил.
.
Разделим на m, и подставим численные значения величин.
;
;
.
(BC.1)   .
Мы получили дифференциальное уравнение движения груза на участке BC.

2.2. Решение уравнения движения

Уравнение (BC.1) является дифференциальным уравнением второго порядка, не содержащим зависимую переменную x в явном виде.

Решаем его с помощью понижения порядка. Для этого выразим вторую производную координаты по времени через первую производную , то есть через проекцию скорости на ось :
. Подставляем в (BC.1).
(BC.2)   .
Это дифференциальное уравнение первого порядка с начальным условием: при .

Интегрируем уравнение (BC.2).

.
Итак, мы получили общее решение уравнения (BC.2):
.
Здесь – произвольная постоянная. Найдем ее значение из начального условия. Подставляем :
;
;
.
Тем самым мы нашли закон изменения скорости груза со временем:
(BC.3)   .

Теперь найдем закон движения груза . Для этого выразим скорость через координату: , и подставим в (BC.3):
(BC.4)   .
Это дифференциальное уравнение первого порядка с начальным условием при .

Интегрируем его.


.
Итак, мы нашли общее решение уравнения (BC.4):
.
Постоянную найдем из начального условия. Подставляем :
.
Отсюда . Тем самым мы нашли закон движения груза на участке BC:
.

Ответ

.
Здесь t выражено в секундах; x – в метрах.

Автор: Олег Одинцов.     Опубликовано: 19-12-2020