Дифференциальные уравнения, не разрешенные относительно производной, приводящиеся к уравнению Бернулли
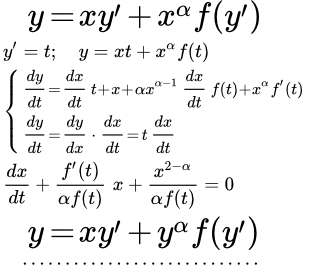
К уравнению Бернулли приводятся уравнения вида:
(1) ;
(2) .
Эти уравнения решаются тем же способом, что и уравнение Лагранжа.
Решение уравнения (1)
Рассмотрим уравнение (1):
(1) .
Будем искать его решение в параметрическом виде. То есть будем считать, что , , а также производная являются функциями от параметра . Положим
.
Поставим в (1):
(3) .
Продифференцируем по :
(4) .
С другой стороны:
(5) .
Поставим (5) в (4) и преобразуем:
;
.
Разделим на . При уравнение принимает вид:
.
Это дифференциальное уравнение Бернулли относительно . Решая его, получаем зависимость . Вместе с уравнением
(3)
оно дает параметрическое представление решения уравнения (1).
Дополнительные решения
В процессе приведения к уравнению Бернулли, мы разделили уравнение на и далее рассматривали решение при . В заключении следует рассмотреть случай . То есть мы должны исключить параметр из уравнений:
;
.
Поставим в последнее уравнение . Тогда уравнение (1) может иметь дополнительные решения, которые определяются из системы уравнений:
То есть дополнительные решения имеют вид:
,
где – корни уравнения
.
Решение уравнения (2)
Аналогично решается уравнение (2):
(2) .
Ищем решение в параметрическом виде. Вводим параметр . Положим
;
Поставим в (2):
(6) .
Продифференцируем по :
(7) .
С другой стороны:
(5) .
Поставим (5) в (7) и преобразуем:
;
(8) .
Из (6), при имеем:
(9) .
Поставим (9) в (8):
.
Делим на . При , и возможно при , уравнение принимает вид:
.
Это дифференциальное уравнение Бернулли относительно . Решая его, получаем зависимость . Вместе с уравнением
(9)
оно дает параметрическое представление решения уравнения (2).
В процессе приведения к уравнению Бернулли, мы разделили уравнение на . Поэтому решение справедливо при . В заключении следует рассмотреть случай . Решая систему
мы можем получить дополнительные решения.
Связь уравнений (1) и (2)
В заключение заметим, что уравнение вида (2) приводится к уравнению вида (1) заменой:
.
Действительно, перепишем уравнение (2):
(2) .
.
Поменяем местами и :
.
Это уравнение вида (1). Как видно, при этом нужно заменить функцию :
.
Автор: Олег Одинцов. Опубликовано: Изменено:
