Свойства функций, непрерывных на отрезке
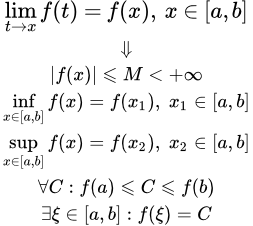
Определения и теоремы
- Функция, непрерывная на отрезке
- Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и непрерывна справа и слева в точках a и b, соответственно.
Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Если функция непрерывна на отрезке ,то она ограничена на этом отрезке.
Доказательство
- Достижимость максимума (минимума) функции на множестве
- Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого
для всех . - Достижимость верхней (нижней) грани функции на множестве
- Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого
.
Легко заметить, что эти определения эквивалентны.
Если и , то .
Если и , то .
Различие между максимумом (минимумом) и верхней (нижней) гранью в том, что максимум (минимум) принадлежит множеству (в данном случае множеству значений функции), а верхняя (нижняя) грань может не принадлежать этому множеству. Пусть, например, на открытом интервале задана функция . На этом интервале функция имеет верхнюю и нижнюю грани:
.
Но максимума и минимума не имеет. Действительно, для любого всегда можно указать такие числа и , принадлежащие , значения функции от которых будут больше и меньше :
.
На отрезке функция имеет как верхнюю и нижнюю грани, так максимум и минимум:
.
Также верхняя (нижняя) грань может равняться плюс (минус) бесконечности: , а максимум (минимум) не может быть бесконечным числом.
Любое множество, в котором определены операции сравнения, имеет верхнюю и нижнюю грани.
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функциядостигает на нем своих верхней и нижней граней или, что тоже самое,
достигает на отрезке своего максимума и минимума.
Доказательство
Эта теорема означает, что существуют такие точки и , принадлежащие отрезку : , значения функции в которых равны, соответственно, нижней и верхней граням:
.
Поскольку, исходя из определений верхней и нижней граней:
при ,
при ,
и поскольку , то и являются минимумом и максимумом функции на отрезке .
Вторая теорема Больцано – Коши о промежуточном значении
Пусть функция непрерывна на отрезке .И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: и .
Тогда существует точка , для которой
.
Доказательство
Следствие 1 (первая теорема Больцано – Коши)
Пусть функция непрерывна на отрезке .И пусть значения функции на концах отрезка имеют разные знаки: или .
Тогда существует точка , значение функции в которой равно нулю:
.
Следствие 2
Пусть функция непрерывна на отрезке .И пусть .
Тогда функция принимает на отрезке все значения из и только эти значения:
при .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
