Решение линейных дифференциальных уравнений первого порядка
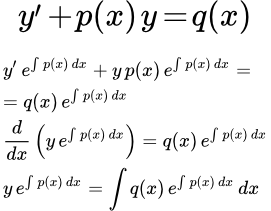
Определения и методы решений
- Линейное дифференциальное уравнение первого порядка
- – это уравнение вида
,
где p и q – функции переменной x.
- Линейное однородное дифференциальное уравнение первого порядка
- – это уравнение вида
.
- Линейное неоднородное дифференциальное уравнение первого порядка
- – это уравнение вида
.
Член q(x) называется неоднородной частью уравнения.
Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:
- метод интегрирующего множителя;
- метод введения двух функций (Бернулли);
- метод вариации постоянной (Лагранжа).
Решение линейного дифференциального уравнения с помощью интегрирующего множителя
Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.
Умножим обе части исходного уравнения (1) на интегрирующий множитель
:
(2)
Далее замечаем, что производная от интеграла равна подынтегральной функции:
По правилу дифференцирования сложной функции:
По правилу дифференцирования произведения:
Подставляем в (2):
Интегрируем:
Умножаем на . Получаем общее решение линейного дифференциального уравнения первого порядка:
Пример решения линейного дифференциального уравнения первого порядка
Решить уравнение
Решение
Разделим обе части исходного уравнения на x:
(i) .
Тогда
;
.
Интегрирующий множитель:
Знак модуля можно опустить, поскольку интегрирующий множитель можно умножать на любую постоянную (в том числе на ± 1).
Умножим (i) на x 3:
.
Выделяем производную.
;
.
Интегрируем, применяя таблицу интегралов:
.
Делим на x 3:
.
Ответ
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
