Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка
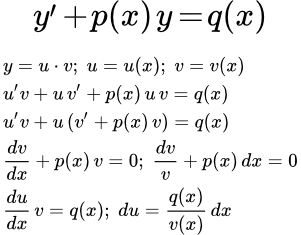
Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
Существует три способа решения этого уравнения:
- метод интегрирующего множителя;
- метод введения двух функций (Бернулли);
- метод вариации постоянной (Лагранжа).
Рассмотрим решение линейного дифференциального уравнения первого порядка методом Бернулли.
Метод введения двух функций (Бернулли)
Ищем решение исходного уравнения в виде произведения двух функций:
y = u · v
где u, v - функции от x. Дифференцируем:
y′ = u′ · v + u · v′
Подставляем в исходное уравнение:
Выносим u за скобки:
(1)
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(2)
Это уравнение с разделяющимися переменными.
Разделяем переменные. Умножаем обе части уравнения на dx и делим на v
Интегрируем:
Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение.
Потенцируем и опускаем знак модуля (Знак модуля сводится к умножению на постоянную ±1).
Подставим в (1) учитывая, что согласно (2), выражение в скобках равно нулю:
Отсюда
Интегрируем
Окончательно находим:
.
Пример решения линейного дифференциального уравнения первого порядка методом Бернулли
Решить уравнение
.
Решение
Делаем подстановку:
y = u · v
где u, v - функции от x. Дифференцируем:
y′ = u′ · v + u · v′
Подставляем в исходное уравнение:
Выносим u за скобки:
(3)
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Это уравнение с разделяющимися переменными,
.
Разделяем переменные. Умножаем обе части уравнения на dx и делим на xv:
Интегрируем:
Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. По таблице интегралов, находим:
Или
Потенцируем и опускаем знаки модуля (Знак модуля сводится к умножению на постоянную ±1).
Подставим в (3) учитывая, что согласно (4), выражение в скобках равно нулю:
Отсюда
Интегрируем, применяя формулу :
.
Окончательно находим:
.
Ответ
Общее решение уравнения:
Автор: Олег Одинцов. Опубликовано: Изменено:
